CSPJ 教学总结：树状数组

cspj

字数统计: 6.1k阅读时长: 25 min

 2025/04/26 

引言

有些时候，题目给我们 N 个元素的序列，然后让我们求前缀和或者区间和。并且，题目还会动态地修改这个序列的值。如果我们每次暴力求解前缀和，时间复杂度会是 O（N），而使用树状数组，可以将查询前缀和的复杂度降低到 O(LogN)。

树状数组是挺不好教学的一个知识点。它需要以下前置知识：

二进制表示法及熟练的位操作
前缀和的知识
树的基础知识
时间复杂度的估算

在教学的时候，我们的教学顺序如下：

先引入问题
lowbit 函数讲解
树状数组的结构特点
利用树状数组求前缀和的方法
怎么修改树状数组的值
如何初始化树状数组
增加值或替换值
二维的树状数组

那么让我们来开始。

问题的引入

P3374 树状数组 1 是一道标准的树状数组问题：该题目给我们了一个数列，我们需要解决以下两个问题：

数列的区间求和
更新某一个数（加上 x）

我们很容易想到用暴力的方法来做此题。于是我们可以估计一下暴力的时间复杂度：

数列的区间求和，时间复杂度 O（N）
更新某一个数，时间复杂度 O（1）

题目中提到，求和的次数最多为 M 次，所以最坏情况下，时间复杂度为 O(M*N)。而由于 M 和 N 的最大范围为 5*10^5，所以最大运算次数高达 (5*10^5) * (5*10^5) = 2500亿次，而竞赛中估算 1000 万次的运算时间就接近 1 秒了，这个时间肯定会超时。

数列的区间求和有一个 O（1）的办法，就是提前求出前缀和。假如 Sum(i) 表示前 i 个数的和，那么区间 (i,j] 的和就可以通过 Sum(j) - Sum(i) 来得出。可惜的是，本题还有一个操作是更新某一个数。如果更新的是第一个数，那么整个前缀和数组 Sum 都需要更新，这样更新的时间复杂度会变成 O（N），最坏情况下会有 O(M*N)次更新，造成运算同样超时。

由此，我们需要一个更优秀的数据结构来解决这类问题，这就是树状数组。

lowbit 函数

在讲解树状数组前，我们先学习一下 lowbit 函数。

lowbit 函数实现的功能是：求 x 的二进制最低位 1 以及后面的 0 组成的数。例如：

8 (10 进制) = 1000 (2 进制) ，则 lowbit(8) = 8
9 (10进制）= 1001（2 进制），则 lowbit(9) = 1
10（10 进制）= 1010（2 进制），则 lowbit(10) = 2

所以，我们需要找到目标数的二进制中的最后那个 1 的位置。有两种实现方式：

方法一：`x^(x-1) & x`

方法一相对比较好理解，我拿二进制数 1100 举例解释如下：

(x-1)的效果，相当于把二进制的最后一个1变成 0，比如某数 1100 减 1之后，就变成了 1011
这个时候，如果我用 x^(x-1),就会得到 1100^1011=0111
最后，用 x& 刚刚的 x^(x-1)，就相当于把x的最后一个1留下来了，前面的1都抹掉了：1100 & 0111 = 0100

方法二：`x&-x`

我们还是拿二进制数 1100 举例，由于负数是用补码表示，所以对于 1100，它的负数：

原码为：11100(最高为 1 为符号位)
反码为：10011(反码符号位不变，其余位取反)
补码为：10100（补码=反码+1）

这样一操作，x&-x 就等于 01100 & 10100 = 0100，同样把最后的 1 取出来了。

在实现中，我们用方法二的更多，因为更短。参考代码如下：

1
2
3

int lowbit(int x) {
    return x & -x;
}

树状数组的定义

对于一个长度为 N 的序列，为了满足上面提到的更快的区间求和和更新的需求，我们可以构造一个树状数组。

树状数组（Binary Index Tree，简称 BIT）通过构造另一个长度为 N 的数组，来做到：

区间求和，时间复杂度 O(log N)
更新某一个数，时间复杂度 O(log N)

因为树状数组需要另外创建一个长度为 N 的数组，所以它的空间复杂度为O(N)。

我们先创建出这个数组 b ，然后再引入它的元素间的树状逻辑关系。

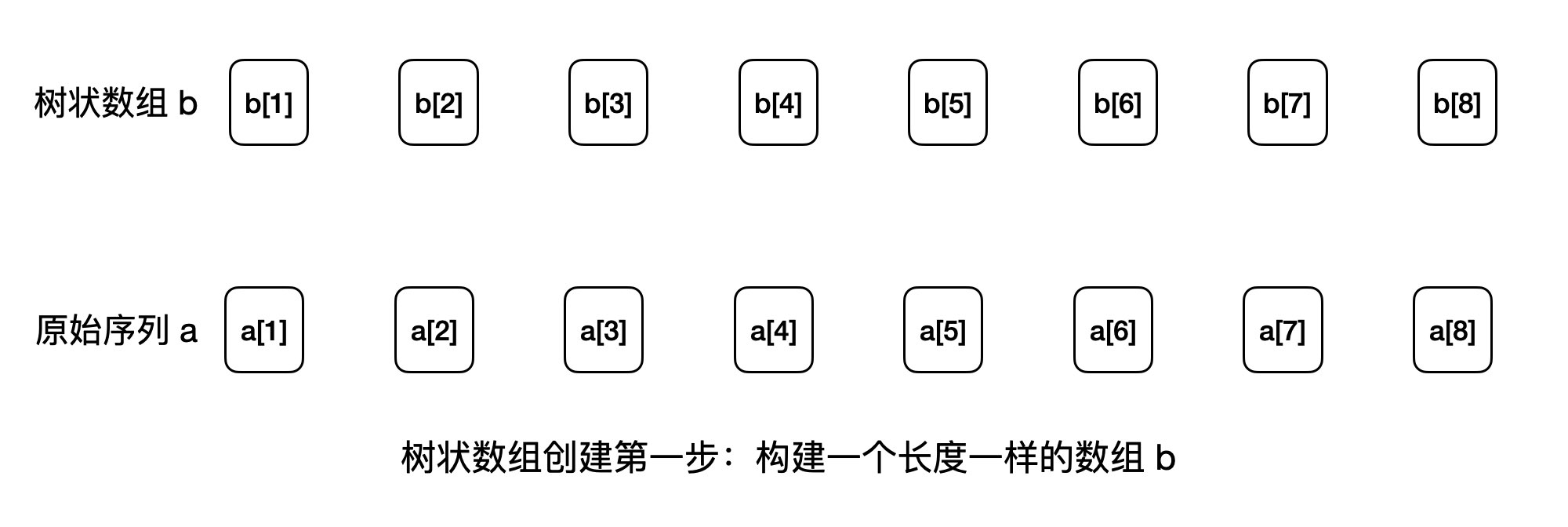
我们有了数组 b，我们让数组 b 相对于原始序列 a，按如下的关系来保存范围和：

b[1] 保存 a[1]的值
b[2] 保存区间 [a[1], a[2]] 的和
b[3] 保存 a[3]的值
….省略若干行
b[8] 保存区间 [a[1], a[8]] 的和

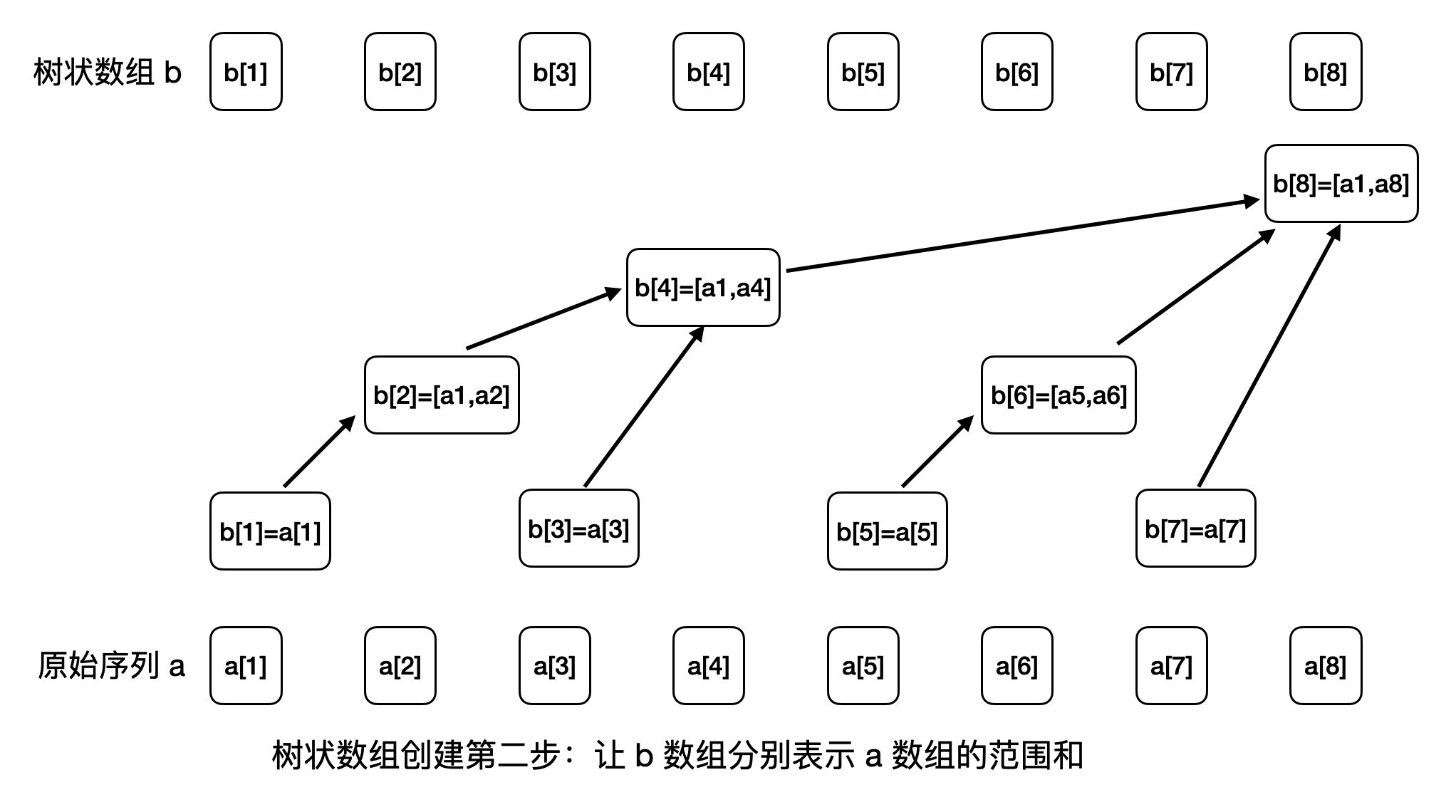
我们先不管如何做到的，先假设我们按上面的逻辑，初始化好了这个数组，那么它怎么能快速求出前缀和呢？

树状数组求和

我们假设要求 a[1] ~ a[7]的和，如下图所示，我们知道这段和满足：Sum(7) = b[4] + b[6] + b[7]

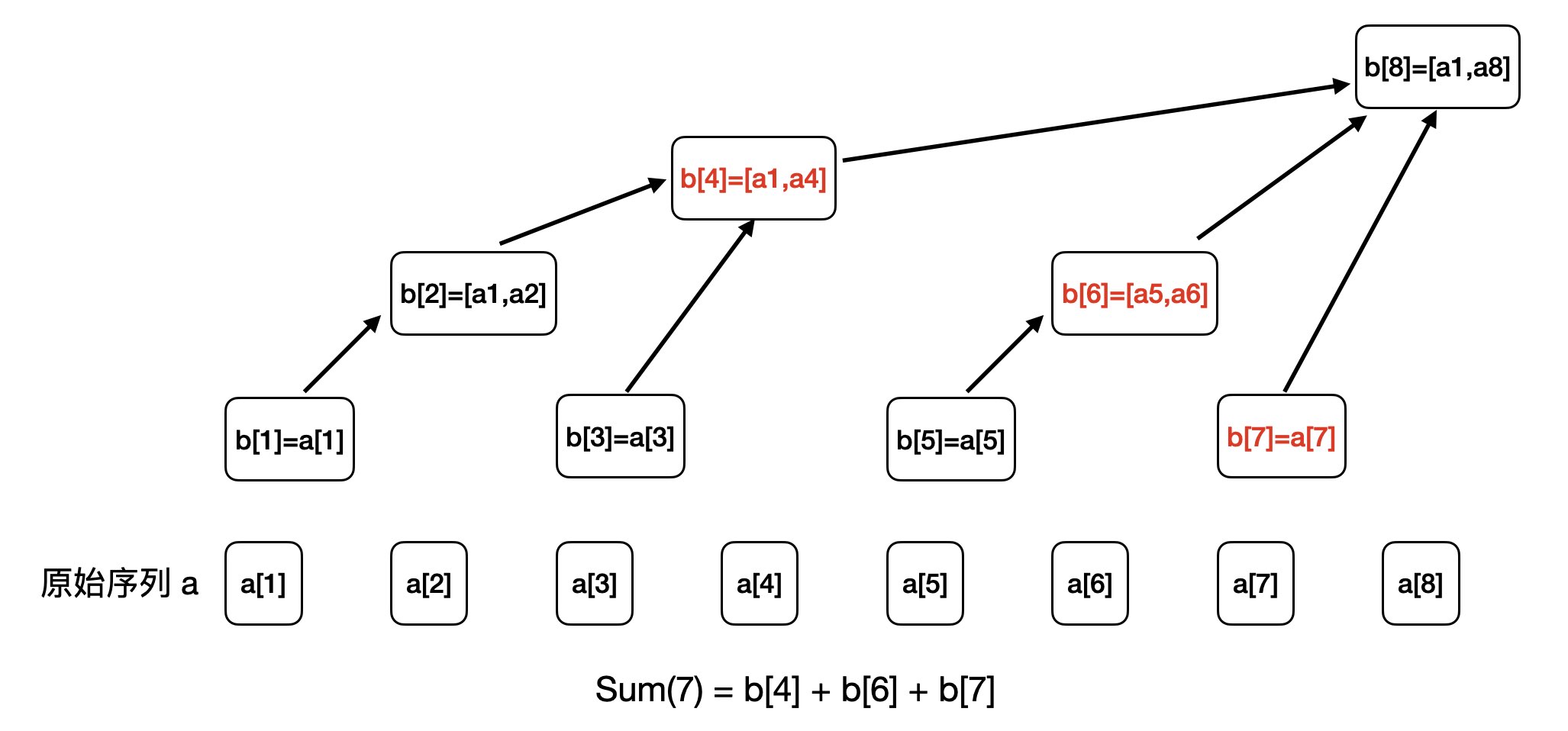
那么，我们观察一下 b[4],b[6],b[7] 这几个下标有什么特点：

4 的二进制：0100
6 的二进制：0110
7 的二进制：0111

如果结合上我们刚刚教的 lowbit 函数，我们就可以发现如下规律：

4 的二进制：0100，4 = 6 - lowbit(6)
6 的二进制：0110，6 = 7 - lowbit(7)
7 的二进制：0111

于是，如果我们要求 Sum(7)，就可以用 b[7] 开始累加，然后用 7 - lowbit(7) 得到 6，再用 6 - lowbit(6) 得到 4，最后 4 - lowbit(4) = 0，就结束整个求和累加过程。

把以上逻辑转换成代码，是这样的：

int query(int range) {
    int ret = 0;
    while (range > 0) {
        ret += b[range];
        range -= lowbit(range);
    }
    return ret;
}

有人可能要问了，这个求和都是从序列开头开始的，如果我们想求序列中间一段，比如从 x 到 y 的区间和，应该怎么办呢？这种情况，我们可以：

用 query(y) 把从头到 y 位置的和求出来
用 query(x-1) 把从头到 x-1 位置的和求出来
然后相减 query(y) - query(x-1) 得到区间 [x,y] 的和

更新数据

树状数组也支持更新数据，像P3374 树状数组 1题目中要求的那样，我们可以将某个数加上 x，这种情况应该如何更新数组呢？

我们以更新 a[1]为例，通过观察，我们发现涉及 a[1] 的数组有：b[1],b[2],b[4],b[8]，如下图所示：

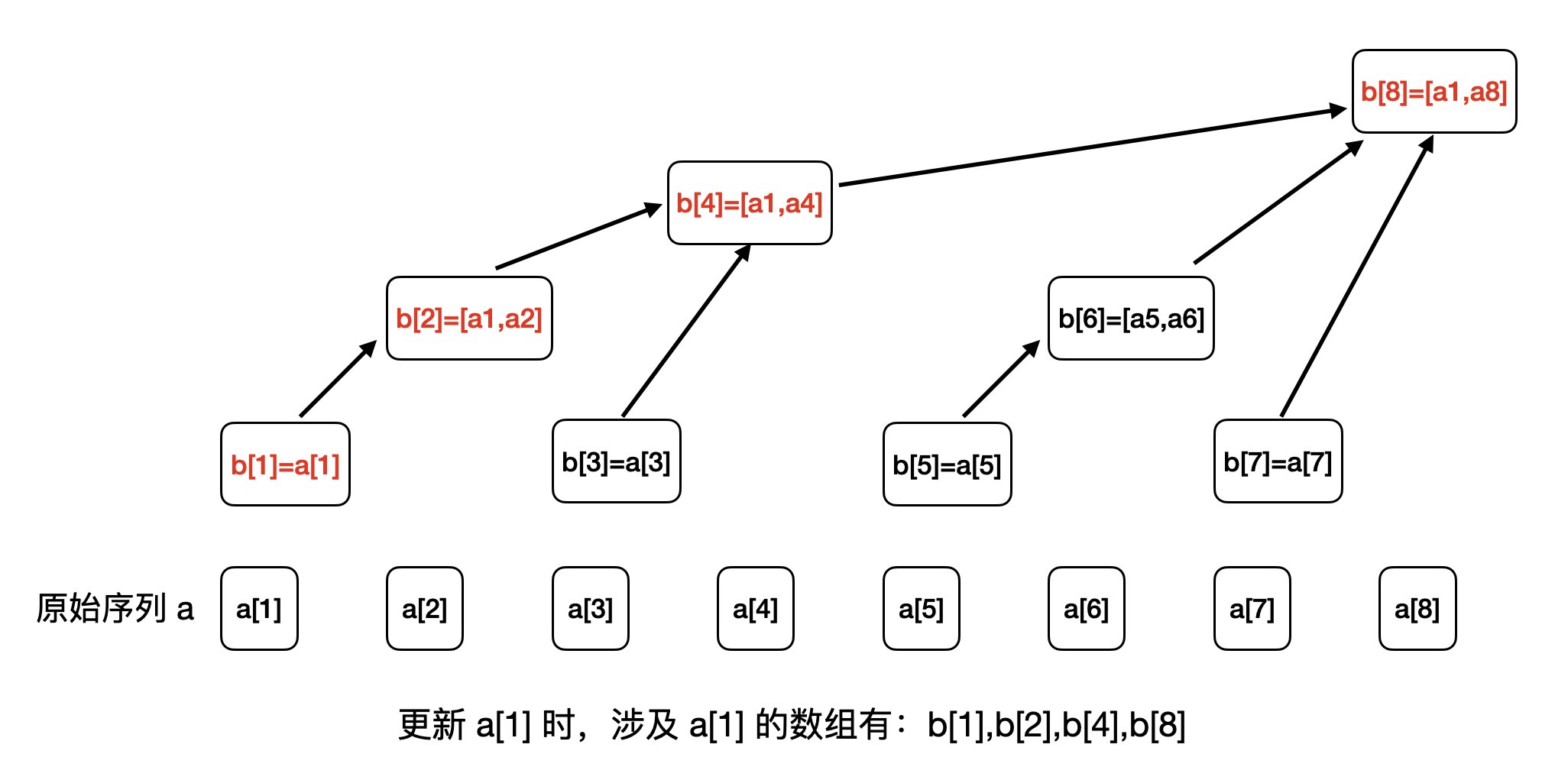
你有观察出来规律吗？这刚好是我们构建的这个树从叶子结点到根结点的一条路径。

那同样的问题来了，我们如何求解出b[1],b[2],b[4],b[8]这个路径呢？我们来观察一下：

1 的二进制是：0001
2 的二进制是：0010, 2 = 1 + lowbit(1)
4 的二进制是：0100, 4 = 2 + lowbit(2)
8 的二进制是：1000, 8 = 4 + lowbit(4)

我们再验证一个中间结点的更新，比如更新 a[5]，如下图所示：

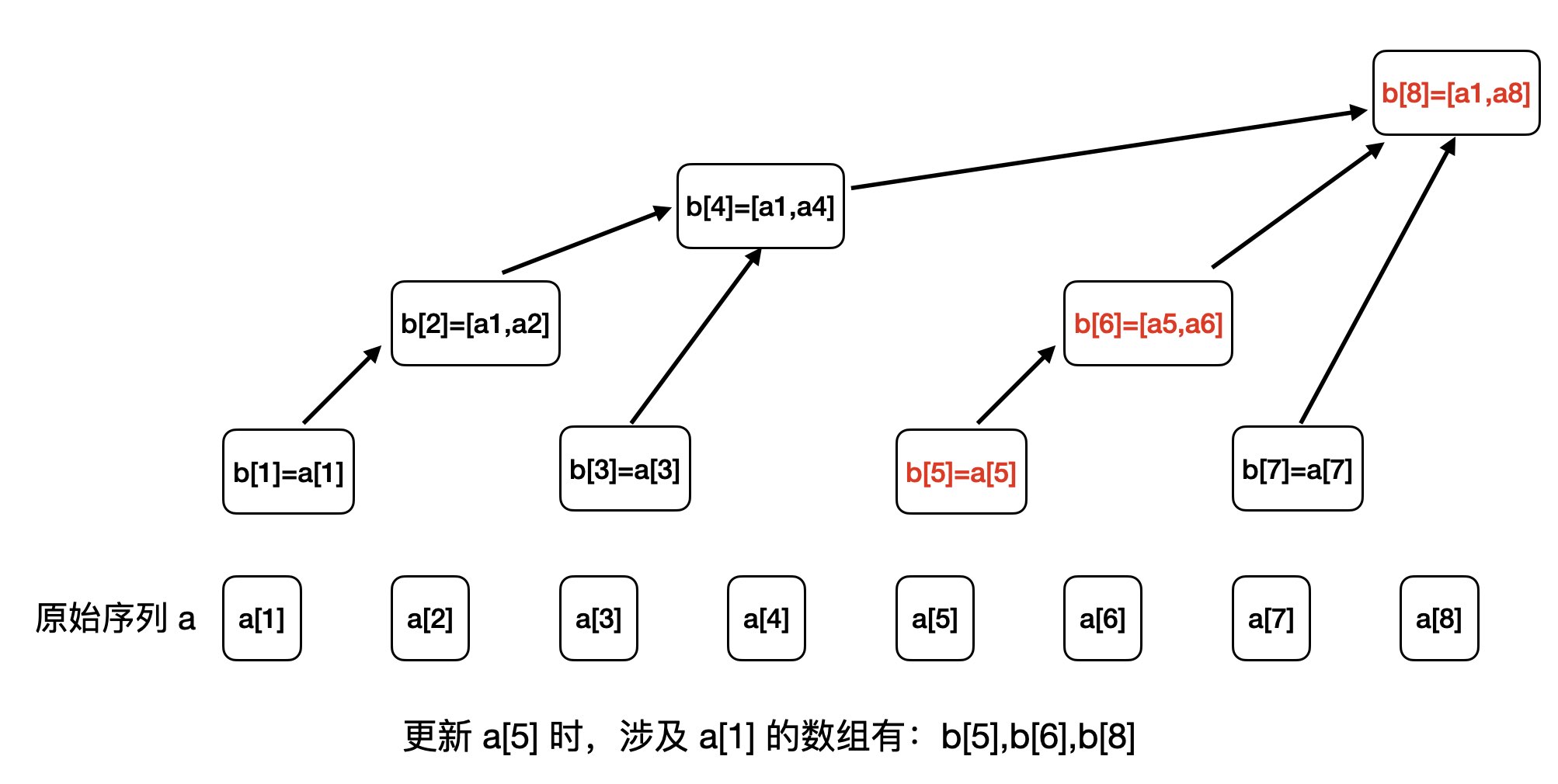
我们看看规则是不是一样：

5 的二进制是 0101，
6 的二进制是 0110，6 = 5 + lowbit(5)
8 的二进制是 1000，8 = 6 + lowbit(6)

至此，我们总结出更新方法：从数列的下标 idx 开始，不停地更新，并且用 idx += lowbit(idx) 获得下一个更新的下标，直到更新到下标超过上界（N）为止。

void add(int idx, int val) {
    while (idx <= n) {
        b[idx] += val;
        idx += lowbit(idx);
    }
}

初始化

最暴力的初始化方法是：我们假设原序列全是 0，这样树状数组的初始状态也全是 0 即可正常表达上面的树型关系。然后，我们把每一个 a 序列中的数用更新的方式来放入树状数组中。

至此，我们完成了例题P3374 树状数组 1中的所有细节讨论，完整的代码如下：

/**
 * Author: Tang Qiao
 */
#include <bits/stdc++.h>
using namespace std;
#define MAXN (int)(500000+10)

int n, m;
int a[MAXN], b[MAXN];

int lowbit(int x) {
    return x & -x;
}

void add(int idx, int val) {
    while (idx <= n) {
        b[idx] += val;
        idx += lowbit(idx);
    }
}

int query(int range) {
    int ret = 0;
    while (range > 0) {
        ret += b[range];
        range -= lowbit(range);
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin >> n >> m;
    for (int i = 1; i <=n; ++i) {
        cin >> a[i];
        add(i, a[i]);
    }
    for (int i = 1; i <= m; ++i) {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1) {
            add(x, y);
        } else {
            cout << query(y) - query(x-1) << endl;
        }
    }
    return 0;
}

但是，以上的这种初使化方法，时间复杂度为 O(N*logN)，如果数据刚好卡在初始化中，我们可以用以下这种方法来将初始化时间复杂度优化到 O(N)。

初始化（优化）

为了讲明白这种初始化，我们需要观察树状数组 b 中的每个元素代表的数据范围有什么规律。为什么 b[5] 只代表 a[5] 一个元素，但是 b[8]代表的是[a[1],a[8]] 区间的 8 个元素的和？

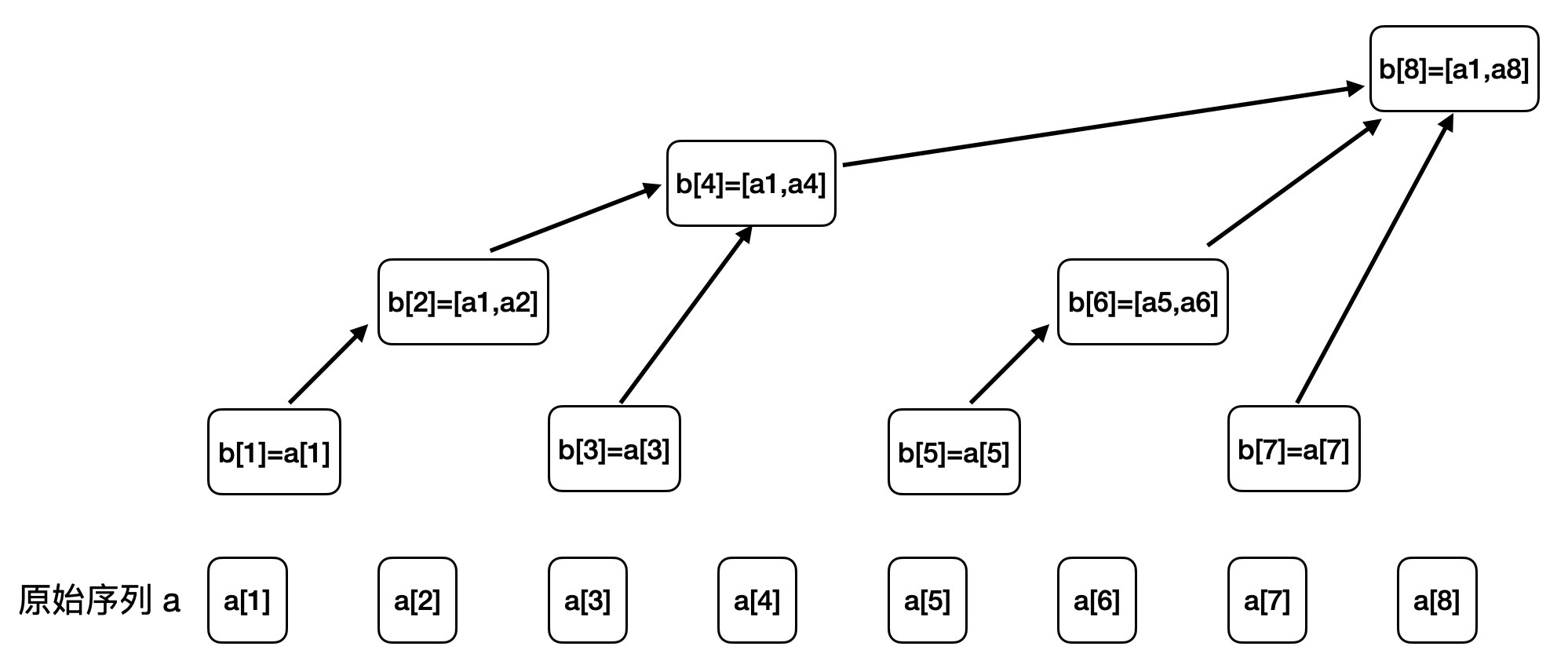
最终我们可以发现，一个数组元素代表的区间范围大小就是它的 lowbit 函数求出来的值。

例如：

lowbit(5) = 1，所以它只代表 a[5] 一个元素
lowbit(8) = 8，所以它代表 [a[1],a[8]] 共 8 个元素
一个十进制数 88，其二进制为 01011000，lowbit(88)=8，所以它代表的区间为 8 个元素。

进一步的，我们可以观察出，对于一个 b[x]，它代表的区间为[x-lowbit(x)+1, x]。

这对初始化有什么用呢？

我们如果构建了数组 a 的前缀和数组 s，s[i]表示前 i 个数的和。
那么，我们就可以用前缀和数组 s 来初始化 b[x]。

因为 b[x] 代表的区间和是[x-lowbit(x)+1, x],所以：b[i] = s[i] - s[i-lowbit(i)]

至此，我们可以将例题P3374 树状数组 1的代码更新如下：

/**
 * Author: Tang Qiao
 */
#include <bits/stdc++.h>
using namespace std;
#define MAXN (int)(500000+10)

int n, m;
int a[MAXN], b[MAXN], s[MAXN];

int lowbit(int x) {
    return x & -x;
}

void add(int idx, int val) {
    while (idx <= n) {
        b[idx] += val;
        idx += lowbit(idx);
    }
}

int query(int range) {
    int ret = 0;
    while (range > 0) {
        ret += b[range];
        range -= lowbit(range);
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin >> n >> m;
    for (int i = 1; i <=n; ++i) {
        cin >> a[i];
        s[i] = s[i-1] + a[i];
    }
    // 初始化
    for (int i = 1; i<=n; ++i) {
        b[i] = s[i] - s[i-lowbit(i)];
    }
    for (int i = 1; i <= m; ++i) {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1) {
            add(x, y);
        } else {
            cout << query(y) - query(x-1) << endl;
        }
    }
    return 0;
}

管辖区间

上面讲到，树状数组中的元素 b[x] 管辖的区间和是[x-lowbit(x)+1, x]，因此，我们更能理解树状数组的更新逻辑：

所谓的更新a[x]，就是把管辖区间涵盖 a[x] 的所有 b[x]都更新一遍。
那哪些 b[x]的管辖区间涵盖 a[x]呢？就是从二进制看，就是范围中有 lowbit(x) 的数。

举例来说，如果我们要更新 a[2] 的值，lowbit(2) 的值是 0010，所以，我们要更新：

b[2], 因为 2 的二进制是 0010，管辖区间是 [1, 2]，宽度是 2
b[4], 因为 4 的二进制是 0100，管辖区间是 [1, 4]，宽度是 4
b[8], 因为 8 的二进制是 1000，管辖区间是 [1, 8]，宽度是 8

再举一个例子，如果我们要更新 a[5] 的值，lowbit(5) 的值是 0001，所以我们要更新：

b[5]，因为 5 的二进制是 0101，管辖区间是 [5, 5]，宽度是 1
b[6]，因为 6 的二进制是 0110，管辖区间是 [5, 6]，宽度是 2
b[8]，因为 8 的二进制是 1000，管辖区间是 [1, 8]，宽度是 8

再举一个例子，如果我们要更新 a[7] 的值，lowbit(7) 的值是 0001，所以我们要更新：

b[7]，因为 7 的二进制是 0111，管辖区间是 [7, 7]，宽度是 1
b[8]，因为 8 的二进制是 1000，管辖区间是 [1, 8]，宽度是 8

通过上面的例子，我们可以看到，管辖区间在更新的过程中宽度是不断扩大的。不同的数，宽度扩大的倍数不同。但至少是每次翻倍的方式来扩大。

我们再从另一个角度来看管辖区间：我们把数状数组的第 1 个到第 56 个元素的二进制列出来，如下所示：

我们可以观察到：bit 为 1 的位置越低，管辖的区域越小，所以：

有一半管辖区域大小为 1 的数（图中为粉色）
剩下的一半，有一半管辖区域大小为 2 的数（图中为绿色）
再剩的一半，有一半管辖区域大小为 4 的数（图中为紫色）
再剩的一半，有一半管辖区域大小为 8 的数（图中为黄色）

再看这些数的间隔：

粉色的间隔是 2-1，每 2 个出现一次
绿色的间隔是 4-1，每 4 个出现一次
紫色的间隔是 8-1，每 8 个出现一次
黄色的间隔是 16-1，每 16 个出现一次

所以，其实树状数组是把区间和数据按分治的思想进行了切分，这样可以快速求和。

另外，从管辖区域的角度考虑，每一个数在进行 lowbit 减运算的时候，得到的新数，一定和之前的区间不是重叠的。我们可以这样证明：

每个元素 b[x] 管辖的区间和是[x-lowbit(x)+1, x]
我们令 y = x - lowbit(x), 则 b[y] 的管辖区间就是：[y-lowbit(y)+1, y],即：[y-lowbit(y)+1, x - lowbit(x)]
可以看到，这两个区间 [y-lowbit(y)+1, x - lowbit(x)] 和 [x-lowbit(x)+1, x]其实是相邻的。

所以，每次减 lowbit(x) 的运算，其实是获得了其左侧相邻的一块区间的和。

我们来看一个查询和的例子，如果我们要求前缀和 sum(7)：

我们先计算 b[7]，7 的二进制是 0111，管辖区间是 [7, 7]，宽度是 1
我们再计算 b[6]，6 的二进制是 0110，管辖区间是 [5, 6]，宽度是 2
我们再计算 b[4]，4 的二进制是 0100，管辖区间是 [1, 4]，宽度是 4

我们从上面的例子可以看到：由于每次减掉的都是最小的一个 lowbit 位，所以左侧相邻的新区间一定更宽。所以求和过程中， b[7],b[6],b[4] 对应的管辖宽度从 1 到 2 再到 4.

我们再看一个前缀和 sum(9) 的例子：

我们先计算 b[9], 9 的二进制是 1001，管辖区间是 [9, 9]，宽度是 1
我们再计算 b[8], 9 的二进制是 1000，管辖区间是 [1, 8]，宽度是 8

和我们刚刚得到的结论相同：求和过程中，随着不断地减 lowbit(x)，获得的新区间更宽。

小结：

树状数组中的元素 b[x] 管辖的区间和是[x-lowbit(x)+1, x]
每次加 lowbit(x) 的过程，相当于在不断扩展管辖区间。不同的数，宽度扩大的倍数不同。但至少是每次翻倍的方式来扩大。
每次减 lowbit(x) 的过程，相当于在查找紧临 b[x] 管辖区间的一块新区间。这个新区间，宽度也是不断扩大的。不同的数，宽度扩大的倍数不同。但至少是每次翻倍的方式来扩大。

差分数组

有些时候，题目会让我们一次更新一段区间，这个时候，我们可以引入差分数组来替代原数组。

差分数组中的每一个元素，是原数组相邻两个数的差。

例如：

原数组： 1,2,3,4,5,6
差分数组：1,1,1,1,1,1

我们对差分数组求前缀和，就可以还原出原数组。

这个时候，如果我们把原数组的第 3 个数到第 5 个数都加上 2，我们看看效果：

原数组： 1,2,5,6,7,6
差分数组：1,1,3,1,1,-1

我们观察到，原数组的一个区间都加上 2 之后，在差分数组那里，只有第 3 个数和第 6 个数有变化，其它都没有变化。所以，如果我们用差分数组来代替原数组，就可以只更新两个数值来代表原来的范围更新。

P3368 【模板】树状数组 2此题可以很好地练习差分数组与数状数组的结合运用，相关代码如下：

/**
 * 差分：
 *  - 假设 A 序列为原序列
 *  - 差分数列 C 为原序列每两个数之间的差
 *    - 即：c[i] = a[i] - a[i-1]
 *         c[1] = a[1]
 *         c[2] = a[2] - a[1]
 *         c[3] = a[3] - a[2]
 *  - 所以：
 *    - a[i] = sum(c[1]+c[2]+...c[i])
 * 
 * 对于本题，如果把数组变成差分数组：
 *  - [x,y] 每个数加上 k，等价于:
 *    - c[x] += k
 *    - c[y+1] -= k
 *  - 求第 a[x] 的值，等价于：
 *    - sum(c[1]+c[2]+...c[x])
 *    - 即求前缀和
 * 
 * Author: Tang Qiao
 */
#include <bits/stdc++.h>
using namespace std;
#define MAXN (int)(500000+10)

int n, m;
int a[MAXN], c[MAXN], b[MAXN];

int lowbit(int x) {
    return x&-x;
}

void add(int idx, int v) {
    while (idx <= n) {
        b[idx] += v;
        idx += lowbit(idx);
    }
}

int query(int range) {
    int ret = 0;
    while (range) {
        ret += b[range];
        range -= lowbit(range);
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        c[i] = a[i] - a[i-1];
        add(i, c[i]);
    }
    while (m--) {
        int op, x, y, k;
        cin >> op;
        if (op == 1) {
            cin >> x >> y >> k;
            add(x, k);
            add(y+1, -k);
        } else {
            cin >> x;
            cout << query(x) << endl;
        }
    }
    return 0;
}

二维的树状数组

刚刚讲到，对于一个 b[x]，它代表的区间为[x-lowbit(x)+1, x]

那么对于一个二维的树状数组 b[x, y]，它代表的区间就是 a(x-lowbit(x)+1, y-lowbit(y)+1) - a(x, y) 形成的矩阵的总和。如下图所示：

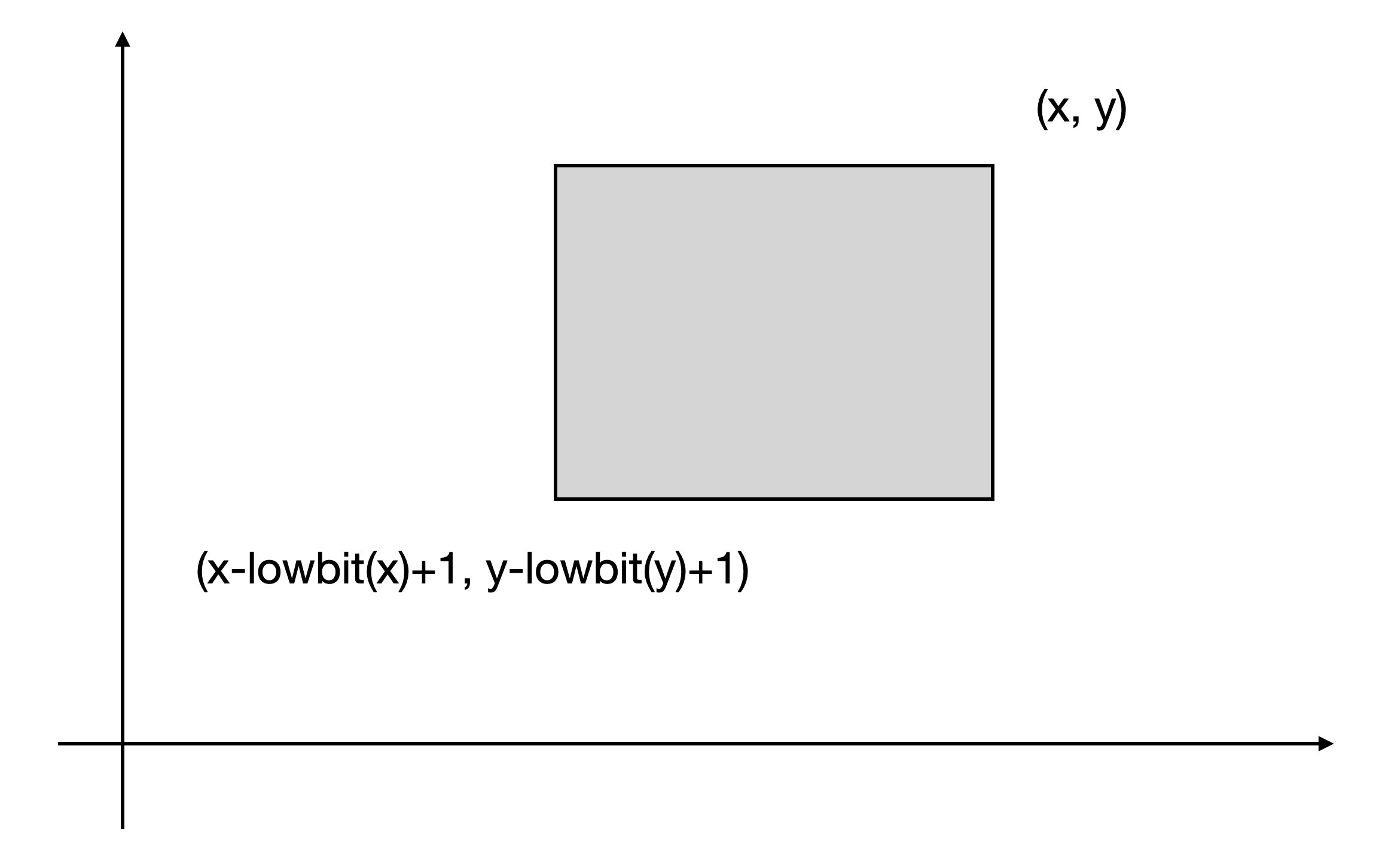
对于二维的树状数组，更新就需要用两层的循环了。示例代码如下：

void add(int x, int y, int v) {
  for (int i = x; i <= n; i += lowbit(i)) {
    for (int j = y; j <= m; j += lowbit(j)) {
      c[i][j] += v;
    }
  }
}

查询前缀和同样需要用循环，示例代码如下：

int query(int x, int y) {
  int res = 0;
  for (int i = x; i > 0; i -= lowbit(i)) {
    for (int j = y; j > 0; j -= lowbit(j)) {
      res += c[i][j];
    }
  }
  return res;
}

如果题目要求区间和，则需要用容斥原理来求解，这里不再展开介绍。

用树状数组求逆序对

什么是逆序对？逆序对是指一个序列中，a[i] > a[j] 且 i < j 的有序对。

比如一个序列是 3 2 1，它的逆序对就有：3 2,3 1,2 1 三组。

树状数组如何和逆序对的数量扯上关系呢？

拿序列 3 2 1 举例，我们知道，树状数组是可以用前缀和的。如果我们：

假设序列初始情况下为全 0
当处理第一个数 3 的时候，我们让树状数组的下标 3 加 1：update(3, 1)，同时记录插入了 1 个数
当处理第二个数 2 的时候，我们统计小于等于 2 的前缀和：query(2)，然后拿总数减 query(2)，得到大于 2 的数字数量
这个数量，就是当 2 被处理的时候，前面有一共多少个数大于 2，即与 2 能够组成逆序对的数量

例题：P1908 逆序对

在此题中，我们先要解决两个问题，才能借用上面的思想：

问题1、题中的数据范围太大，我们如何解决?

答案：我们可以用离散化的思想，把 2 10000 1 变成 2 3 1，因为逆序对是统计相对大小，所以这样更改之后，逆序对的数量是不变的。

具体如何离散化呢？我们可以将数据依次标记上编号，然后排序。例如：

原始序列为 100 200 50, 我们把它分别标上编号 (100,1), (200,2), (50,3)
然后我们将数值排序，得到：(50,3), (100,1), (200,2)
然后，我们再将新的序列赋上从 1 开始的编号：(50,3,1), (100,1,2), (200,2,3)
然后，我们再将序列按原来的编号(第 2 个数字）排序，得到 (100,1,2), (200,2,3), (50, 3, 1)
至此，我们转换得到了新的编号 2,3,1

因为 N 最多是 5*10^5，所以离散化之后，树状数组的大小也缩减到了 5*10^5

在实现的时候，我们可以用结构体来保存上面的三元组。

struct Node {
    int v;
    int origin_idx;
    int next_idx;
};

问题2、如果有两个相等的元素，会不会计算错误？

我们假设元素是 200 300 200,按我们刚刚的操作：

先标号，得到 (200,1) (300,2) (200,3)
再排序，得到 (200,1) (200,3) (300,2)
再标号，得到 (200,1,1) (200,3,2) (300,2,3)
再排序，得到 (200,1,1) (300,2,3) (200,3,2)
最后序列是 1,3,2

这种是没问题的，但是，如果我们排序的时候不是用的稳定排序，把第二个 200 排到了前面，就会得到 2,3,1，这样逆序对就会多一个 2 1，而这本来是不存在的。

所以，为了解决这个问题，我们可以用稳定排序stable_sort，或者保证排序的时候，值相同的情况下，标号大的在后面。

以下是完整的参考程序：

/**
 * Author: Tang Qiao
 */
#include <bits/stdc++.h>
using namespace std;

#define MAXN (int)(5*1e5+10)

struct Node {
    int v;
    int origin_idx;
    int next_idx;
};
Node a[MAXN];
int n,c[MAXN];
long long ans;

bool comp1(const Node &a, const Node &b) {
    return a.v < b.v;
}

bool comp2(const Node &a, const Node &b) {
    return a.origin_idx < b.origin_idx;
}

int lowbit(int x) { return x&-x; }

void add(int a, int v) {
    while (a<=n) {
        c[a]+=v;
        a+=lowbit(a);
    }
}

int query(int a) {
    int ret = 0;
    while(a) {
        ret += c[a];
        a -= lowbit(a);
    }
    return ret;
}


int main() {
    cin >> n;
    for (int i = 1; i <=n; ++i) {
        cin >> a[i].v;
        a[i].origin_idx = i;
    }
    stable_sort(a+1, a+1+n, comp1);
    for (int i = 1; i<=n; ++i) 
        a[i].next_idx = i;
    stable_sort(a+1, a+1+n, comp2);

    for (int i = 1; i <=n; ++i) {
        add(a[i].next_idx, 1);
        ans += i - query(a[i].next_idx);
    }
    cout << ans << endl;

    return 0;
}

题目	描述
B3874 小杨的握手问题	GESP 202309 六级真题
-	-