CSPJ 教学思考：并查集

cspj

字数统计: 1.7k阅读时长: 6 min

 2025/02/09 

并查集在引入之前，需要先教会学生集合的概念。

集合

集合是数学中的一个基本概念，它是由一些确定的、彼此不同的对象所组成的整体。集合有两个特点：

集合中的元素是互不相同的。
集合中的元素没有顺序之分。比如集合 {1, 2, 3} 和 {3, 2, 1} 是同一个集合。

生活中的集合有很多，比如：班级，家庭成员，朋友等等。所以，学生还是比较容易理解的。

并查集

并查集是一种用于管理元素所属集合的数据结构，实现为一个森林，其中每棵树表示一个集合，树中的节点表示对应集合中的元素。

并查集支持两种操作：

查询（Find）：查询某个元素所属集合（查询对应的树的根节点），这可以用于判断两个元素是否属于同一集合
合并（Merge）：合并两个元素所属集合（合并对应的树）

在教学并查集的时候，画示意图可以很好地让学生理解并查集的操作。

并查集的初始化

我们用数组来表示并查集，用数组的值表示当前结点的父亲。如下图所示：

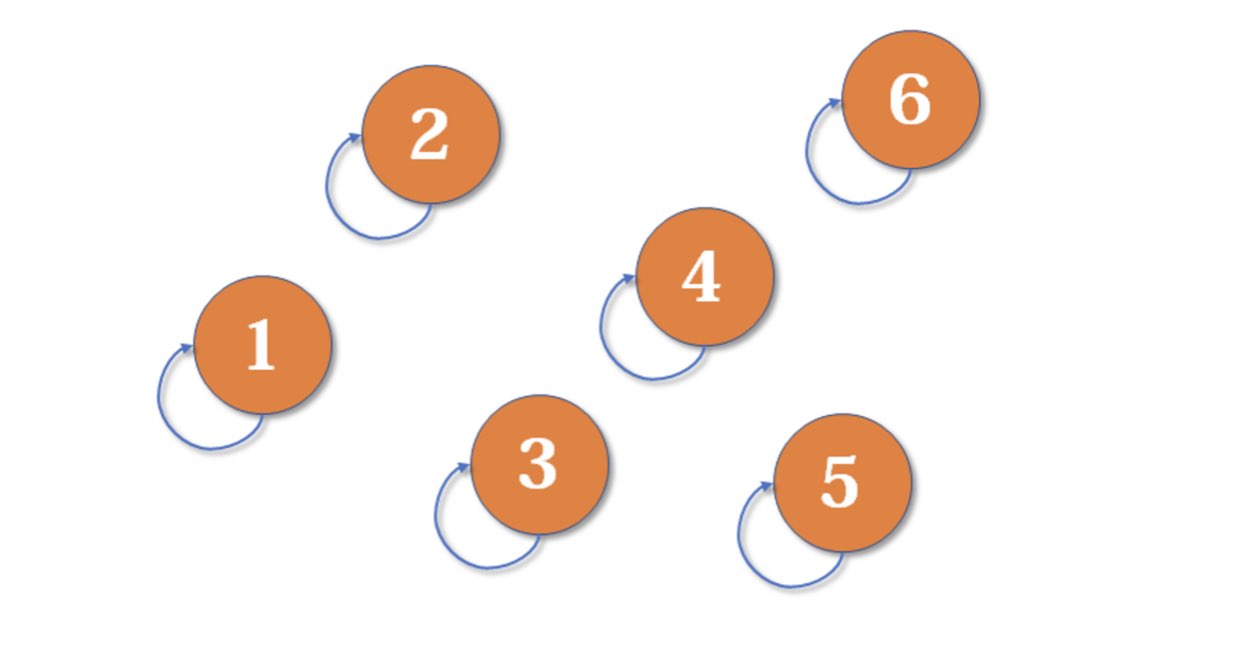
所以，初始化的代码如下：

#define MAXN 1010

int p[MAXN], n;
void init() {
    for (int i = 0; i <= n ; ++i) {
        p[i] = i;
    }
}

并查集的查询操作

并查集在查询时，从初始结点开始，判断自己是不是根结点。根结点的特征是自己是自己的父亲。如果自己不是根结点，则继续递归往上找。示例代码如下：

int find(int a) {
    if (p[a] == a) return a;
    return find(p[a]);
}

我们在这儿，也顺便引入路径压缩的优化，告诉学生在返回值的时候，如果更新结点，就可以把下图中的长路径“拍扁”，使得下次查询的时候速度更快。

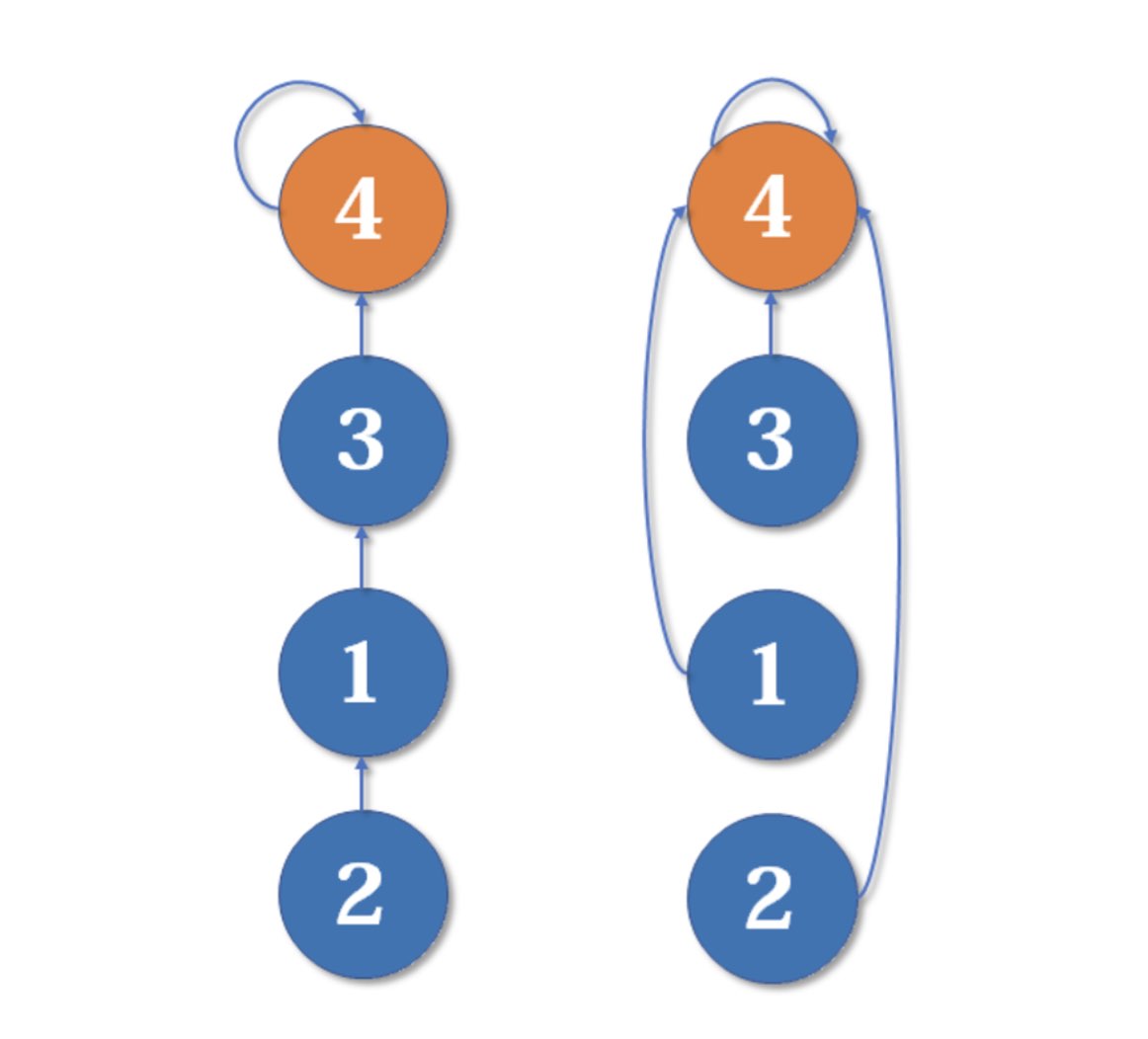
那么如何更新呢？只需要在上面的代码基础上做一点点改动，如下：

int find(int a) {
    if (p[a] == a) return a;
    return p[a] = find(p[a]); // 在返回值之前，更新结点值
}

以上代码可以简化成一行：return p[a]==a ? a : (p[a] = find(p[a]));。但是教学的时候，还是展开让学生理解清楚后，再提供简化的写法比较好。

并查集的合并操作

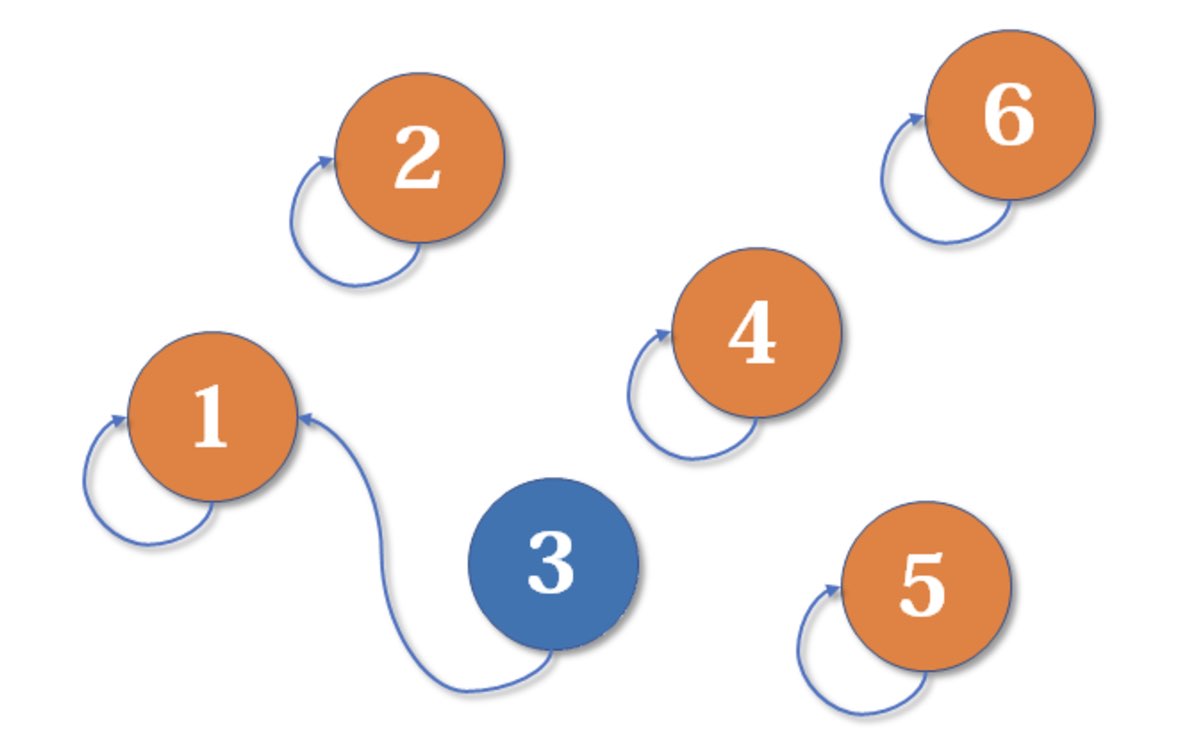
合并的时候，像上图那样，我们把一个结点的根结点的父亲，指向另外一个根结点即可。

void merge(int a, int b) {
    int pa = find(a);
    int pb = find(b);
    p[pa] = pb;
}

以上代码可以简化成一行：p[find(a)]=find(b);。但是教学的时候，还是展开让学生理解清楚后，再提供简化的写法比较好。

判断并查集中集合的个数

因为有一个根结点，就代表有一个集合，所以我们可以数根结点的个数来得到集合的个数。

根结点的特点是：它的父结点就是自己。相关代码如下：

int cnt = 0;
for (int i = 1; i <=n; ++i) {
    if (p[i] == i) {
        cnt++;
    }
}

并查集的练习题

完成以上的基础教学，就可以练习了。并查集的考查主要就是两个：

判断两点是否联通
计算连通块（集合）的个数

以下是基础的练习题目。

题目	说明
P1551 亲戚	基础题
P1536 村村通	基础题
P1892 团伙	提高题，需要用反集

反集

当题目中引入了敌人关系，并且定义：“敌人的敌人是朋友”的时候，就可以用反集来求解了。

反集专门用于表示敌对关系，并且敌人的敌人是朋友。反集的思路是再构造一个集合（称之为反集），然后将“敌人”关系通过原集和反集表示出来。

我们看个例子：

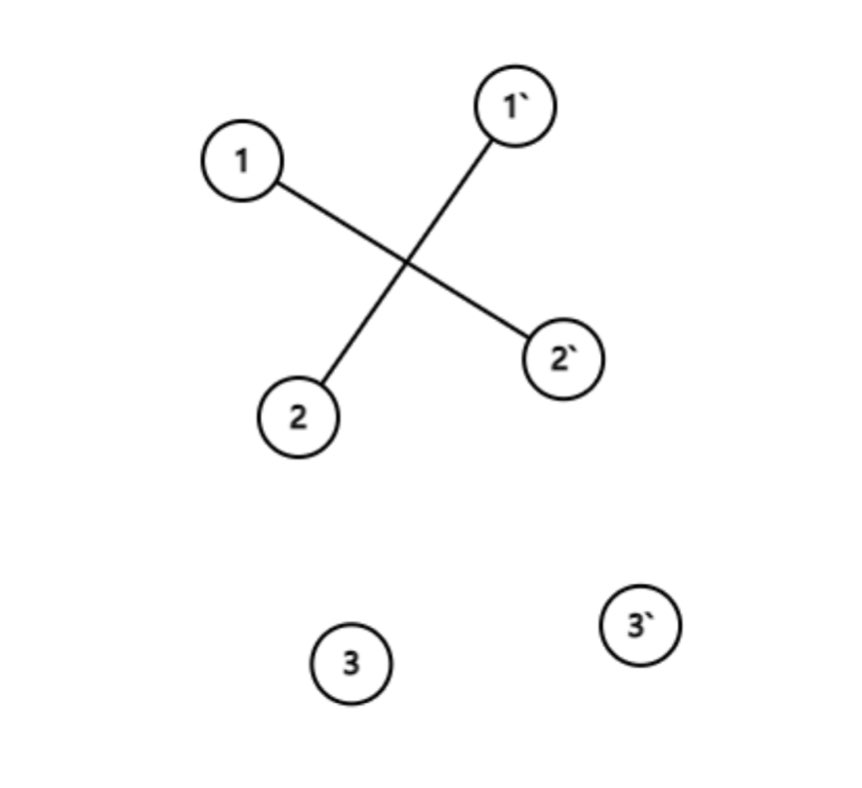
比如假设有 3 个元素，1, 2, 3。我们称他们的反集元素分别为 1' , 2', 3'; 分别表示 1, 2, 3 的敌人。

这个时候，如果 1 和 2 是敌人，则：

因为 1' 也是 1 的敌人, 所以 1' 和 2 是朋友
因为 2' 也是 2 的敌人, 所以 2' 也是 1 的朋友

结果表示如下：

这个时候，如果 2 和 3 是敌人，则

2 和 3` 是朋友
3 和 2` 是朋友

结果表示如下：

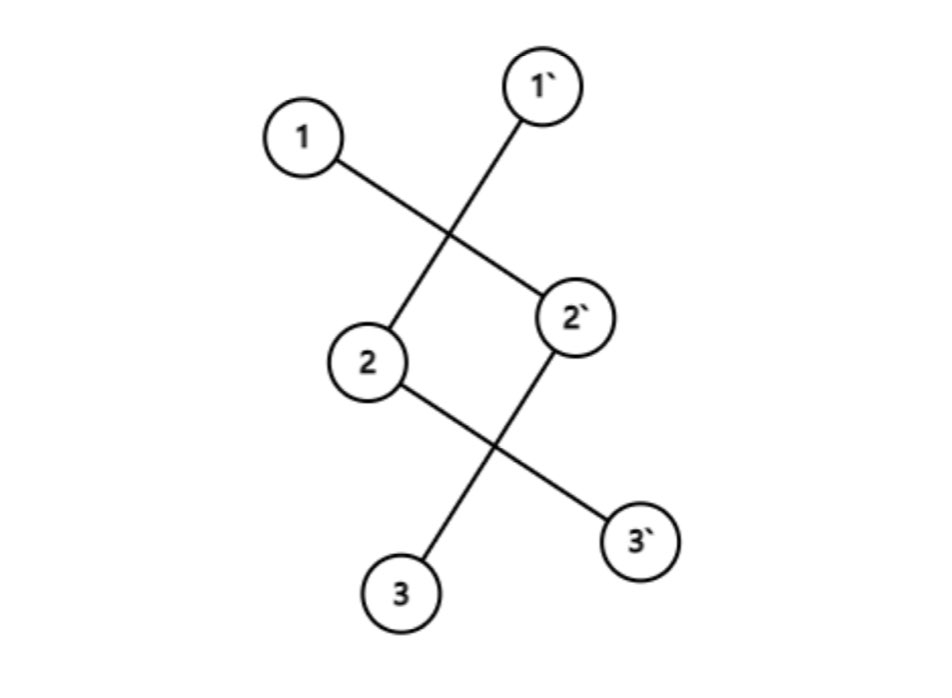
我们可以看到，在这种操作下，1 和 3 自然就在一个集合中了（成为朋友了）。

以上逻辑在并查集中如何实现呢？我们将并查集的下标扩展一倍，用 n+1 ~ 2n 来表示反集元素。其中，元素 a 的反集是 a+n。

这个时候，如果 a 与 b 是敌人，则需要在并查集中做如下操作：

因为 a 与 b 是敌人，所以 a 与 b+n 就是朋友，需要 merge(a, b+n);
因为 a 与 b 是敌人，所以 b 与 a+n 就是朋友，需要 merge(b, a+n);

P1892 团伙是反集的典型例题，可以拿此题练习。

需要特别注意的是，因为此题需要判断集合数量，所以需要让 1~n 的元素当根结点，涉及合并操作的时候，不要让 1~n 的元素当反集元素的孩子。关健代码如下：

void merge(int a, int b) {
    int fa = find(a);
    int fb = find(b);
    // b 有可能是反集，所以始终让 fb 在合并的时候当子结点
    p[fb] = fa; 
}

P1892 团伙的完整参考代码如下：

#include <bits/stdc++.h>
using namespace std;

int p[2010], n, m;

int find(int a) {
    if (p[a] == a) return a;
    return p[a] = find(p[a]);
}

void merge(int a, int b) {
    int fa = find(a);
    int fb = find(b);
    // b 有可能是反集，所以始终让 fb 在合并的时候当子结点
    p[fb] = fa; 
}

int main() {
    for (int i = 0; i < 2010; ++i) {
        p[i] = i;
    }
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; ++i) {
        char ch[3];
        int a, b;
        scanf("%s%d%d", ch, &a, &b);
        if (ch[0] == 'F') {
            merge(a, b);
        } else {
            merge(a, b+n);
            merge(b, a+n);
        }
    }
    int cnt = 0;
    for (int i = 1; i <=n; ++i) {
        if (p[i] == i) {
            cnt++;
        }
    }
    printf("%d\n", cnt);

    return 0;
}