唐巧的博客

CSPJ 教学思考：动态规划

cspj
字数统计: 6.9k阅读时长: 34 min
2025/01/05

引言

动态规划是 CSPJ 拉分的关键知识点。

之所以这样，是因为动态规划不像 DFS、BFS、二分那样有固定的模版格式。学生要在动态规划问题上融汇贯通，需要花费大量的练习，也需要足够的聪明。

笔者自己在高中阶段，也是在动态规划问题上困扰许久。我自己的学习经验是：动态规划还是需要多练，练够 100 道题目，才能够熟悉动态规划的各种变型。之后在比赛中看到新的题目，才会有点似曾相识的感觉，进一步思考出状态转移方程。

所以，我打算写 100 道动态规划方程的题解，希望有志攻破此难关的学生和家长一起加油！

动态规划解题的核心问题

虽然动态规划没有模版可以套，但是动态规划有三个核心问题：

  • 状态的定义
  • 状态转移方程
  • 初始状态的设置

一般思考动态规划就是思考以上三个问题，这三个问题解决了，动态规划的程序也可以写出来了。

教学题目

推荐的教学题目如下：

题目名 说明
P2842 纸币问题 1 基础 DP，记忆化搜索
P1216 数字三角形 基础 DP，记忆化搜索 【经典 DP】
P2840 纸币问题 2 基础 DP
P2834 纸币问题 3 基础 DP，有多处可优化的点
P1048 采药 NOIP2005 普及组第三题。01 背包问题。【经典 DP】
P1616 疯狂的采药 完全背包问题。【经典 DP】
P2196 挖地雷 NOIP1996 提高组第三题。涉及输出路径技巧。
P1434 滑雪 上海市省队选拔 2002
P1115 最大子段和 最大子段和。【经典 DP】

适合的作业：

题目名 说明
P4017 最大食物链计数 记忆化搜索
P2871 Charm Bracelet S USACO 07 DEC，01 背包
P1802 5 倍经验日 01 背包
P1002 过河卒 NOIP2002 普及组，记忆化搜索
P1049 装箱问题 NOIP2001 普及组，01 背包
P1064 金明的预算方案 01 背包变型，NOIP2006 提高组第二题
P1077 摆花 NOIP2012 普及组
P1164 小A点菜 与摆花一题类似
P2392 考前临时抱佛脚 01 背包变型

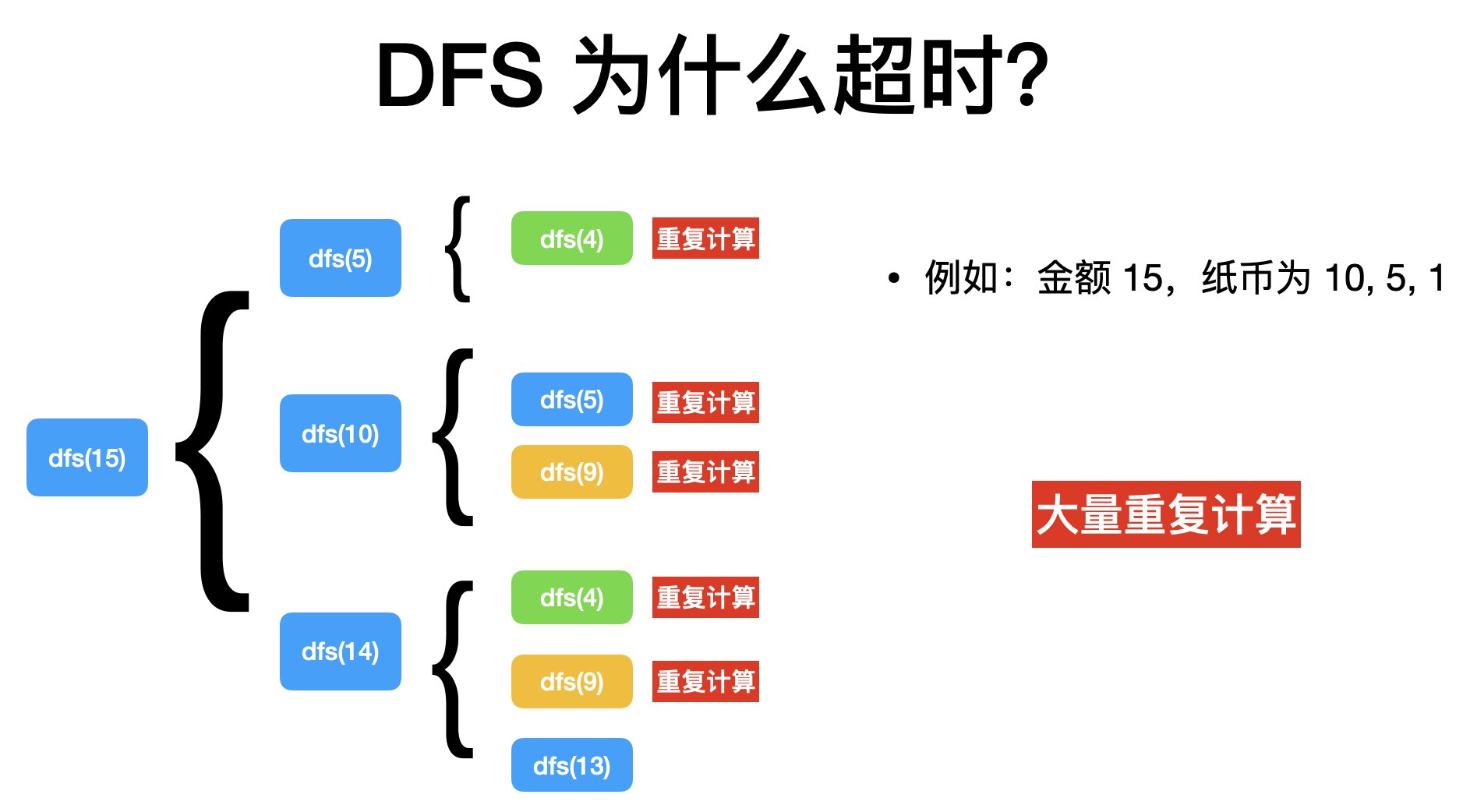
例题代码

P2842 纸币问题 1

此题可以带着孩子一步步推导和演进。具体步骤如下。

先引导孩子用最暴力的 DFS 的方式来做此题，建立基础的解题框架，虽然会超时，但是也帮助我们后面引导孩子学会记忆化搜索。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * DFS，超时
 */
#include <bits/stdc++.h>
using namespace std;

int n, w;
int v[1100];

int dfs(int pt) {
    if (pt == 0) return 0;
    int ret = 1e9;
    for (int i = 0; i < n; ++i) {
        if (pt>=v[i]) {
            ret = min(ret, dfs(pt-v[i]) + 1);
        }
    }
    return ret;
}

int main() {
    scanf("%d%d", &n, &w);
    for (int i = 0; i < n; ++i) {
        scanf("%d", v+i);
    }
    int ans = dfs(w);
    printf("%d\n", ans);
    return 0;
}

有了上面的代码，通过分析，发现大部分的超时是因为有重复的计算过程。以下是一个以 10,5,1 为例的示意：

所以，我们可以将重复计算的过程保存下来，以后再次需要计算的时候，直接读取保存的结果即可。在此思想下，我们只需要在上面改动三行，即可将超时的程序改为通过。具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * DFS，记忆化搜索
 */
#include <bits/stdc++.h>
using namespace std;

int n, w;
int v[1100];
int r[10010]; // 改动 1

int dfs(int pt) {
    if (pt == 0) return 0;
    if (r[pt] != 0) return r[pt]; // 改动 2

    int ret = 1e9;
    for (int i = 0; i < n; ++i) {
        if (pt>=v[i]) {
            ret = min(ret, dfs(pt-v[i]) + 1);
        }
    }
    return (r[pt]=ret); // 改动 3
}

int main() {
    scanf("%d%d", &n, &w);
    for (int i = 0; i < n; ++i) {
        scanf("%d", v+i);
    }
    int ans = dfs(w);
    printf("%d\n", ans);
    return 0;
}

有了以上两段代码的尝试，我们能够发现：

  • dfs(pt) 只与 dfs( 0 ~ pt-1) 有关,与 dfs(pt+1~w)无关。
  • 如果我们知道了 dfs(0~pt)，就可以推出 dfs(pt+1)

那么，我们就可以思考，如果我们用 dp[i] 来表示钱币总额为 i 的结果数。那么，dp[i] 的计算过程（即：状态转移方程）为：dp[i] = min( dp[i-v[j]] )+1，其中j=0~N。

这样，我们就可以引导学生写出第一个动态规划程序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * dp[i] = min( dp[i-v[j]] )  + 1 
 */
#include <bits/stdc++.h>
using namespace std;

int n, w;
int v[1100], dp[11000];

int main() {
    scanf("%d%d", &n, &w);
    for (int i = 0; i < n; ++i) {
        scanf("%d", v+i);
    }
    memset(dp, 0x3f, sizeof(dp));
    dp[0] = 0;
    for (int i = 1; i <=w ; ++i) {
        for (int j = 0; j < n; ++j) {
            if (i-v[j]>=0) {
                dp[i] = min(dp[i], dp[i-v[j]]+1);
            }
        }
    }
    printf("%d\n", dp[w]);
    return 0;
}

P1216 数字三角形

P1216 数字三角形同样可以用记忆化搜索引入。先写记忆化搜索的代码有助于我们理解动态规划的状态转移方程。

搜索的代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * DFS，记忆化
 */
#include <bits/stdc++.h>
using namespace std;

int n;
int v[1010][1010];
int r[1010][1010];

int dfs(int x, int y) {
    if (r[x][y] != -1) return r[x][y];
    if (x == n-1) return 
        r[x][y] = v[x][y];
    else return 
        r[x][y] = v[x][y]+max(dfs(x+1,y), dfs(x+1,y+1));
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j <= i; ++j) {
            scanf("%d", &v[i][j]);
        }
    }
    memset(r, -1, sizeof(r));
    printf("%d\n", dfs(0, 0));
    return 0;
}

由搜索代码可知，每一个位置的最价结果由它下面两个结点的最价结果构成。于是，我们可以构造出状态转移方程：dp[i][j] = v[i][j] + max(dp[i+1][j], dp[i+1][j+1])

另外，我们可以引导学生：上层的依赖于下层的数据，那应该怎么推导呢？让学生想到用倒着 for 循环的方式来从下往上推导。

最后，我们再引导学生构建一下初始值。由此，我们建立起动态规划解题的三个核心问题：

  • 状态的定义
  • 状态转移方程
  • 初始状态的设置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * 动态规划：
 * dp[i][j] = v[i][j] + max(dp[i+1][j], dp[i+1][j+1])
 */
#include <bits/stdc++.h>
using namespace std;

int n;
int v[1010][1010];
int dp[1010][1010];

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j <= i; ++j) {
            scanf("%d", &v[i][j]);
        }
    }
    // 初始状态
    for (int j = 0; j < n; ++j) {
        dp[n-1][j] = v[n-1][j];
    }
    // dp
    for (int i = n-2; i>=0; --i) {
        for (int j = 0; j <= i; ++j) {
            dp[i][j] = v[i][j] + max(dp[i+1][j], dp[i+1][j+1]);
        }
    }
    printf("%d\n", dp[0][0]);
    return 0;
}

P2840 纸币问题 2

状态转移方程为：dp[i] = sum(dp[i- v[j]]), j = 0~N，结果需要每次模 1000000007。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <bits/stdc++.h>
using namespace std;

int n, w;
int v[1010], dp[10010];

int main() {
    scanf("%d%d", &n, &w);
    for (int i = 0; i < n; ++i) {
        scanf("%d", v+i);
    }
    dp[0] = 1;
    for (int i = 1; i <= w ; ++i) {
        dp[i] = 0;
        for (int j = 0; j < n; ++j) {
            if (i >= v[j]) {
                dp[i] = (dp[i] + dp[i-v[j]])%1000000007;
            }
        }
    }
    printf("%d\n", dp[w]);
    return 0;
}

P2834 纸币问题 3

此题不能像之前的题目那样，用金钱数为阶段。因为此题是计算的组合数，所以 1,5 和 5,1 是一种答案。如果以金钱数为阶段，就无法方便将这种重复计算的排除掉。

那么，以什么为阶段，可以保证每个阶段可以基于过去的阶段推导出来？可以用不同的钱币种类为阶段！

接下来就是思考这种情况下的状态转移方程。可以得出，状态转移方程如下：

  • dp[i][j] 表示用前 i 种钱币组成金额 j 的组合数
  • dp[i][j] = dp[i-1][j-v[i]] + dp[i-1][j - v[i]*2] + …. dp[i-1][j-v[i]*n]; (j >= v[i]*n)
  • 初始状态：dp[1][0] = 1; dp[1][v[1]] = 1; dp[1][v[1]*2] = 1;

参考程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <bits/stdc++.h>
using namespace std;

const int MOD = 1000000007;
int n, w;
int v[1010], dp[1010][10010];

int main() {
    scanf("%d%d", &n, &w);
    for (int i = 0; i < n; ++i) {
        scanf("%d", v+i);
    }
    memset(dp, 0, sizeof(dp));
    // dp[0][0] = 1; dp[0][v[0]] = 1;dp[0][v[0]*2] = 1;….
    int cnt = 0;
    while (cnt <= w) {
        dp[0][cnt] = 1;
        cnt += v[0];
    }
    for (int i=1; i<n; ++i) {
        for (int j=0; j<=w; ++j) {
            cnt = 0;
            while (j - cnt >= 0) {
                dp[i][j] = (dp[i][j]+dp[i-1][j-cnt]) % MOD;
                cnt += v[i];
            }
        }
    }
    printf("%d\n", dp[n-1][w]);
    return 0;
}

此题还有另外一种状态转移方程，把阶段分为没有用过 a，和至少用过一张 a。

这样的话，状态转移方程优化为：dp[i][j] = dp[i-1][j] + dp[i][j-v[i]]

这样，代码的复杂度进一步降低，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;

const int MOD = 1000000007;
int n, w;
int v[1010], dp[1010][10010];

int main() {
    scanf("%d%d", &n, &w);
    for (int i = 0; i < n; ++i) {
        scanf("%d", v+i);
    }
    memset(dp, 0, sizeof(dp));
    int cnt = 0;
    while (cnt <= w) {
        dp[0][cnt] = 1;
        cnt += v[0];
    }
    for (int i=1; i<n; ++i) {
        for (int j=0; j<=w; ++j) {
            if (j-v[i]>=0) {
                dp[i][j] = (dp[i-1][j]+dp[i][j-v[i]])% MOD;	
            } else {
                dp[i][j] = dp[i-1][j];
            }
        }
    }
    printf("%d\n", dp[n-1][w]);
    return 0;
}

此题还可以进一步简化，因为 dp[i] 那一层算完之后 dp[i-1] 层就没有用了。有没有可能我们将 dp[i]层和 dp[i-1]都合并在一起呢？

答案是可以的。我们可以将关键代码进一步简化如下，把 dp 改成一个一维数组。状态转移方程变为了:dp[j] = dp[j] + dp[j-v[i]]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;

const int MOD = 1000000007;
int n, w;
int v[1010], dp[10010];

int main() {
    scanf("%d%d", &n, &w);
    for (int i = 0; i < n; ++i) {
        scanf("%d", v+i);
    }
    memset(dp, 0, sizeof(dp));
    int cnt = 0;
    while (cnt <= w) {
        dp[cnt] = 1;
        cnt += v[0];
    }
    for (int i=1; i<n; ++i) {
        for (int j=0; j<=w; ++j) {
            if (j-v[i]>=0) {
                dp[j] = (dp[j]+dp[j-v[i]]) % MOD;	
            } else {
                dp[j] = dp[j]; //此行可以删除，但为了教学示意保留
            }
        }
    }
    printf("%d\n", dp[w]);
    return 0;
}

P1048 采药

P1048 采药这题是经典的 01 背包问题。为了方便教学，我们还是从最简单的动态规划思路开始推导。

我们把每个草药是一个阶段，这样：

  • dp[i][j] 表示前 i 个草药，花费 j 时间可以得到的最大价值
  • 状态转移方程为：dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]])

这样写出来的参考程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
dp[i][j] 表示前 i 个草药，花费 j 时间可以得到的最大价值
dp[i][j] = max(dp[i-1][j], dp[i-1][j-t[i]] 
 */
#include <bits/stdc++.h>
using namespace std;

int T, M;
int t[110], v[110];
int dp[110][1010];

int main() {
    scanf("%d%d", &T, &M);
    for (int i = 1; i <= M; ++i) {
        scanf("%d%d", t+i, v+i);
    }
    // 下标从 1 开始，这样不用考虑 i-1 越界了
    for (int i = 1; i <= M; ++i) {
        for (int j = 1; j <= T; ++j) {
            dp[i][j] = dp[i-1][j];
            if (j - t[i] >= 0) {
                dp[i][j] = max(dp[i][j], dp[i-1][j - t[i]]+v[i]);
            }
        }
    }
    printf("%d\n", dp[M][T]);
    return 0;
}

与上一题一样，通过分析，我们发现 dp[i][j] 中的 i 一层可以优化掉，变成只有 dp[j]。

这样，状态转移方程被优化成：dp[j]=max(dp[j],dp[j-t[i]]+v[i])。

但是，因为每一个草药只能用一次，如果我们正着循环 j 的话，会出现多次使用第 i 个草药的情况。所以，我们倒着进行递推，就可以避免这种情况。

最终实现的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
dp[j] 花费 j 时间可以得到的最大价值
dp[j] = max(dp[j], dp[j-t[i]])
 */
#include <bits/stdc++.h>
using namespace std;

int T, M;
int t[110], v[110];
int dp[1010];

int main() {
    scanf("%d%d", &T, &M);
    for (int i = 1; i <= M; ++i) {
        scanf("%d%d", t+i, v+i);
    }
    for (int i = 1; i <= M; ++i) {
        for (int j = T; j >= t[i]; --j) {
            dp[j] = max(dp[j], dp[j - t[i]]+v[i]);
        }
    }
    printf("%d\n", dp[T]);
    return 0;
}

P2196 挖地雷

P2196 挖地雷 是 NOIP1996 提高组第三题。这道题的解法有点类似于P1216 数字三角形。

但是，这道题更难的是：它需要我们输出路径。

我们先说状态转移方程：

  • dp[i] 表示第 i 个地窖能够挖到的最多地雷数。
  • w[i] 表示第 i 个地窖的地雷数。
  • 转移方程：dp[i] = max(dp[i+1~N]中能够与 dp[i] 连通的地窖) + w[i] 与 dp[i] = w[i]中的较大者。

我们再说说如何输出路径。因为计算之后 dp 数组中保存了每个结点能够挖的最大地雷数。所以，我们从答案 dp[ans]开始，找哪一个地窖与当前相连，同时值又等于 dp[ans] - w[ans],则表示那个地窖是下一个点。

参数代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
using namespace std;

int n;
int w[30];
int v[30][30];
int dp[30];

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", w+i);
    }
    for (int i = 1; i <=n ; ++i) {
        for (int j = i+1; j<=n; ++j) {
            scanf("%d", &v[i][j]);
        }
    }
    int ans = 0;
    for (int i = n; i>=1; --i) {
        dp[i] = w[i];
        for (int j = i+1; j<=n; ++j) {
            if (v[i][j]) {
                dp[i] = max(dp[i], dp[j]+w[i]);
            }
        }
        if (dp[ans] < dp[i]) ans = i;
    }
    int cnt = dp[ans];
    int idx = ans;
    while (cnt) {
        printf("%d ", idx);
        cnt -= w[idx];
        for (int i = idx + 1; i<=n; ++i) {
            if (v[idx][i] && cnt == dp[i]) {
                idx = i;
                break;
            }
        }
    }
    printf("\n%d\n", dp[ans]);
    return 0;
}

P1434 滑雪

这道题的麻烦点是如何定义状态转移的阶段，因为没有明显的阶段。

可以考虑的办法是：将点按高度排序，这样从高度低的点开始，往高的点做状态转移。

所以：

  • 定义：dp[i][j] 表示从 (i,j) 这个位置开始滑的最长坡。
  • 转移方程：
    • dp[x][y] = max(dp[x'][y'])+1
    • dp[x'][y'] 为上下左右相邻并且高度更低的点
  • 初始化：无
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <bits/stdc++.h>
using namespace std;

int r, c;
int tu[110][110];
int dp[110][110];
int movex[]={-1,1,0,0};
int movey[]={0,0,-1,1};
bool debug = false;

struct Node {
    int x, y, h;
    Node(int _x, int _y, int _h) {
        x = _x; y = _y; h = _h;
    }
};
bool operator<(Node a, Node b) {
    return a.h < b.h;
}
vector<Node> v;

int main() {
    scanf("%d%d", &r, &c);
    v.reserve(r*c);
    for (int i = 0; i < r; ++i) {
        for (int j = 0; j < c; ++j) {
            scanf("%d", &tu[i][j]);
            v.push_back(Node(i, j, tu[i][j]));
        }
    }
    sort(v.begin(), v.end());
    memset(dp, 0, sizeof(dp));
    int ans = 0;
    for (int i = 0; i < r*c; ++i) {
        Node node = v[i];
        int x = node.x;
        int y = node.y;
        for (int j = 0; j < 4; ++j) {
        	int tox = x + movex[j];
        	int toy = y + movey[j];
        	if (tox >=0 && tox <r && toy >=0 && toy<c &&
        		node.h > tu[tox][toy]) {
        		dp[x][y] = max(dp[x][y], dp[tox][toy]);
        	}
        }
        dp[x][y] += 1;
        ans = max(ans, dp[x][y]);
        if (debug) {
        	printf("dp[%d][%d]=%d\n", x, y, dp[x][y]);
        }
    }
    printf("%d\n", ans);
    return 0;
}

此题更容易想到的写法还是记忆化搜索：对每一个点作为开始点进行一次 DFS，同时在进行递归调用的时候，如果当前点处理过，则返回上次的结果。

参考代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/**
 * DFS, 记忆化
 */
#include <bits/stdc++.h>
using namespace std;

int r, c;
int tu[110][110];
int rem[110][110];

int movex[]={-1,1,0,0};
int movey[]={0,0,-1,1};

int dfs(int x, int y) {
    if (rem[x][y] != 0) return rem[x][y];
    int mm = 0;
    for (int i = 0; i < 4; ++i) {
        int tox = x + movex[i];
        int toy = y + movey[i];
        if (tox >=0 && tox <r && toy >=0 && toy<c &&
        		tu[x][y] > tu[tox][toy]) {
            mm = max(mm, dfs(tox, toy));
        }
    }
    return (rem[x][y] = mm + 1);
}

int main() {
    scanf("%d%d", &r, &c);
    for (int i = 0; i < r; ++i) {
        for (int j = 0; j < c; ++j) {
            scanf("%d", &tu[i][j]);
        }
    }
    int ans = 0;
    for (int i = 0; i < r; ++i) {
        for (int j = 0; j < c; ++j) {
            ans = max(ans, dfs(i, j));
        }
    }
    printf("%d\n", ans);
    return 0;
}

P1115 最大子段和

P1115 最大子段和 是最经典的一类动态规划问题。思路如下：

  • dp[i] 表示包含 i 这个数，并且以 i 结尾的最大子段和。
  • 状态转移方程：
    • 如果 dp[i-1] 为负数，那么 dp[i] = v[i]
    • 如果 dp[i-1] 为正数，那么 dp[i] = dp[i-1]+v[i]

因为 dp[i] 在转移方程上只与 dp[i-1]相关，所以它最终结构上被可以被化简成类似贪心的策略，即：

  • 用一个变量记录当前的累加值，如果当前累加值为负数，则重新计算。
  • 在累加过程中随时判断，记录最大的累加值为最终答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <bits/stdc++.h>
using namespace std;

int n;
int v[200100];

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        scanf("%d", v+i);
    }
    int cnt = 0;
    int ans = -1e9;
    for (int i = 0; i < n; ++i) {
        cnt += v[i];
        ans = max(ans, cnt);
        if (cnt < 0) cnt = 0;
    }
    printf("%d\n", ans);
    return 0;
}

作业代码

P4017 最大食物链计数

P4017 最大食物链计数最佳的做法是做记忆化的搜索。

记录下出度为 0 的结点，从这些结点开始去寻找，把各种可能的路径加总。同时在 DFS 的时候，记录下搜索的结果。

参考代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * 记忆化搜索
 */
#include <bits/stdc++.h>
using namespace std;

#define MOD 80112002

int n, m;
vector<vector<int> > v;
int r[5010], out[5010];

int dfs(int a) {
    if (r[a] != -1) return r[a];
    // 如果是头部，算一种情况
    if (v[a].size() == 0) return (r[a]=1);
    // 如果不是头部，则求和
    int cnt = 0;
    for (int i = 0; i < v[a].size(); ++i) {
        cnt = (cnt + dfs(v[a][i])) % MOD;
    }
    return r[a] = cnt;
}

int main() {
    memset(r, -1, sizeof(r));
    scanf("%d%d", &n, &m);
    v.resize(n+1);
    for (int i = 0; i < m; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        v[a].push_back(b); // a 被 b 吃
        out[b]++; // b 的出度+1
    }
    int ans = 0;
    for (int i = 1; i <=n ; ++i) {
        // 如果 i 出度为 0，就表示只能被吃，为底部
        if (out[i] == 0) { 
            ans += dfs(i);
            ans %= MOD;
        }
    }
    printf("%d\n", ans);
    return 0;
}

P2871 Charm Bracelet S

P2871 Charm Bracelet S 是最最标准的 01 背包问题。可以作为基础练习。

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <bits/stdc++.h>
using namespace std;

int n, m;
int w[3500], v[3500], dp[14000];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++i) {
        scanf("%d%d", w+i, v+i);
    }
    memset(dp, 0, sizeof(dp));
    for (int i = 0; i < n; ++i) {
        for (int j = m; j>=w[i]; --j) {
            dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
        }
    }
    printf("%d\n", dp[m]);
    return 0;
}

P1802 5 倍经验日

经典的 01 背包问题：

  • dp[i] 表示 i 容量可以获得的最大的经验值增量。
  • w[i] 表示第 i 个药的数量。
  • t[i] 表示第 i 个药贡献的经验值增量。

状态转移方程：dp[j] = max(dp[j], dp[j-w[i]]+t[i])。

需要注意答案最大超过了 int，需要用 long long。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <bits/stdc++.h>
using namespace std;

int dp[1010], w[1010], t[1010];
int base = 0, n, x;

int main() {
    scanf("%d%d", &n, &x);
    for (int i = 0; i < n; ++i) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        base += a;
        t[i] = b-a;
        w[i] = c;
    }
    for (int i=0; i<n; ++i) {
        for (int j=x; j>=0; --j) {
            if (j-w[i]>=0) {
                dp[j] = max(dp[j], dp[j-w[i]]+t[i]);
            }
        }
    }
    //最大结果为 5*1e9，需要用 long long
    printf("%lld\n", 5LL*(dp[x] + base));
    return 0;
}

P1002 过河卒

P1002 过河卒此题是标准的记忆化搜索。有两个陷阱：

  • 马所在的位置也不能走。
  • long long。

相关代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * 记忆化搜索。
 */
#include <bits/stdc++.h>
using namespace std;

int bx, by, hx, hy;
long long r[22][22];

bool block(int x, int y) {
    int v = abs(x-hx)*abs(y-hy);
    return (v == 2 || x==hx && y == hy);
}

long long dfs(int x, int y) {
    if (x>bx || y>by) return 0;
    if (x == bx && y == by) return 1;
    if (r[x][y]!=-1) return r[x][y];
    if (block(x,y)) return r[x][y] = 0;
    long long ans = dfs(x+1,y) + dfs(x,y+1);
    return r[x][y] = ans;
}

int main() {
    memset(r, -1, sizeof(r));
    cin >> bx >> by >> hx >> hy;
    printf("%lld\n",dfs(0, 0));
    return 0;
}

P1064 金明的预算方案

P1064 金明的预算方案 是一道 01 背包的变型题。题目增加了附件的概念，初看起来没法下手，但是题目增加了一个限制条件：附件最多只有 2 个。

所以，我们可以将 01 背包的“选或不选”两种情况扩充成以下 5 种情况：

  • 不选
  • 选主件，不选附件
  • 选主件 + 附件 1
  • 选主件 + 附件 2
  • 选主件 + 附件 1 + 附件 2

然后就可以用 01 背包来实现该动态规划了。我们把每种物品的费用当作背包的体积，把每种物品的价格*权重当作价值。

转移方程是：dp[i]=max(dp[i], 5 种物品选择情况)，每种选择情况下，dp[i]=max(dp[i], dp[i-该选择下的花费]+该选择下的收益) 。

另外，需要注意，输入数据的编号可能不按顺序提供，有以下这种情况：

1
2
3
4
100 3
1000 5 3
10 5 3
50 2 0

以下是参考程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <bits/stdc++.h>
using namespace std;

struct Node {
    int m;
    int w;
    int t;
};

int n, m;
vector<Node> va;
vector<vector<Node> > vb;
int dp[40000];

void updateDP(int i, int m, int w) {
    if (i-m >= 0) {
        dp[i] = max(dp[i], dp[i-m] + w);
    }
}

int main() {
    scanf("%d%d", &n, &m);
    va.resize(m);
    vb.resize(m);
    for (int i = 0; i < m; ++i) {
        Node node;
        scanf("%d%d%d", &node.m, &node.w, &node.t);
        node.w = node.w*node.m; 
        va[i] = node;
        if (node.t != 0) {
            vb[node.t - 1].push_back(node);
        }
    }
    memset(dp, 0, sizeof(dp));
    for (int i = 0; i < m; ++i) {
        // 只处理主件，附件与主体一并处理
        if (va[i].t == 0) {
            for (int j = n; j > 0; j--) {
                // 选主件，不选附件
                updateDP(j, va[i].m,va[i].w);
                // 选主件+附件 1
                if (vb[i].size() > 0) {
                    int money = va[i].m + vb[i][0].m;
                    int weight = va[i].w + vb[i][0].w;
                    updateDP(j, money, weight);
                }
                // 选主件+附件 2
                if (vb[i].size() == 2) {
                    int money = va[i].m + vb[i][1].m;
                    int weight = va[i].w + vb[i][1].w;
                    updateDP(j , money, weight);
                }
                // 选主件+附件 1+附件 2
                if (vb[i].size() == 2) {
                    int money = va[i].m + vb[i][0].m + vb[i][1].m;
                    int weight = va[i].w + vb[i][0].w + vb[i][1].w;
                    updateDP(j, money, weight);
                }
            }	
        }
    }
    cout << dp[n] << endl;
    return 0;
}

P1077 摆花

P1077 摆花 一题是 NOIP2012 普及组的第三题。

  • dp[i][j] 表示前 i 种花，摆在前 j 个位置上的种数。

状态转移方程：

1
2
3
4
dp[i][j] = dp[i-1][j] 不放第 i 种花
         + dp[i-1][j-1] 放 1 个第 i 种花
         + dp[i-1][j-2] 放 2 个第 i 种花
         ...

这道题的难点：没有想到 dp[0][0]=1。因为后面推导的时候，
dp[i-1][j-k] 中 j==k 的时候，也是一种可能的情况，要统计进来。

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <bits/stdc++.h>
using namespace std;

int n, m;
int a[110];
int dp[110][110];

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", a+i);
    }
    memset(dp, 0, sizeof(dp));
    dp[0][0] = 1;
    for (int i = 1; i <= n; ++i) {
        for (int j = 0; j <= m; ++j) {
            for (int k = 0; k <= a[i]; ++k) {
                if (j - k >= 0) {
                    dp[i][j] += dp[i-1][j-k];
                    dp[i][j] %= 1000007;	
                }
            }
        }
    }
    printf("%d\n", dp[n][m]);
    return 0;
}

P1164 小A点菜

P1164 小A点菜一题阶段比较明显。每一道菜点不点是一个明显阶段。所以：

  • dp[i][j]表示前 i 道菜，用 j 的价格，能够点的方案数

对于每道菜，有点或不点两种方案，所以：

  • 转移方程：dp[i][j] = dp[i-1][j]+dp[i-1][j-a[i]]

由于 i 阶段只与 i-1 阶段相关，所以可以把阶段压缩掉，只留一维。最后压缩后的方案是：

  • dp[j] 表示用 j 的价格可以点到的点的种数
  • 初始条件 dp[0] = 1，因为这样才可以把后面的结果递推出来
  • dp[j] = dp[j] + dp[j-a[i]]

因为和 01 背包类似的原因，压缩后需要倒着用 for 循环，否则每道菜就用了不止一次了。

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;

int n, m;
int a[110];
int dp[10010];

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", a+i);
    }
    memset(dp, 0, sizeof(dp));
    dp[0] = 1;
    for (int i = 1; i <= n; ++i) {
        for (int j = m; j>=a[i]; --j) {
            dp[j] += dp[j-a[i]];
        }
    }
    printf("%d\n", dp[m]);
    return 0;
}

P2392 考前临时抱佛脚

P2392 考前临时抱佛脚 此题可以用动态规划，也可以用搜索，因为每科只有最多 20 个题目，所以搜索空间最大是 2^20 等于约 100 万。

以下是搜索的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * 搜索
 */
#include <bits/stdc++.h>
using namespace std;

int s[4], v[25];
int ans, tot, ret;

void dfsAns(int pt, int n, int cnt) {
    if (pt == n) {
        int tmp = max(cnt, tot-cnt);
        ret = min(ret, tmp);
        return;
    }
    dfsAns(pt+1, n, cnt);
    dfsAns(pt+1, n, cnt+v[pt]);
}

int main() {
    scanf("%d%d%d%d", s, s+1, s+2, s+3);
    for (int i = 0; i < 4; ++i) {
        memset(v, 0, sizeof(v));
        tot = 0;
        for (int j = 0; j < s[i]; ++j) {
            scanf("%d", v+j);	
            tot += v[j];
        }
        ret = tot;
        dfsAns(0, s[i], 0);
        ans += ret;
    }
    printf("%d\n", ans);
    return 0;
}

用动态规划解题时，此题可以把每次复习看作一次 01 背包的选择。每道题的价值和成本相同。背包的目标是尽可能接近 sum/2，因为sum 最大值为 20*60 = 1200，所以背包大小最大是 600。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
using namespace std;

int s[4];
int v[25];
int ans = 0;
int dp[610];

int dpAns(int n) {
    int cnt = 0;
    for (int i = 0; i < n; ++i) {
        cnt += v[i];
    }
    int m = cnt / 2;
    memset(dp, 0, sizeof(dp));
    for (int i = 0; i < n; ++i) {
        for (int j = m; j>=v[i]; --j) {
            dp[j] = max(dp[j], dp[j-v[i]] + v[i]);
        }
    }
    int ret = max(dp[m], cnt - dp[m]);
    return ret;
}

int main() {
    scanf("%d%d%d%d", s, s+1, s+2, s+3);
    for (int i = 0; i < 4; ++i) {
        memset(v, 0, sizeof(v));
        for (int j = 0; j < s[i]; ++j) {
            scanf("%d", v+j);	
        }
        ans += dpAns(s[i]);
    }
    printf("%d\n", ans);
    return 0;
}

原文作者：唐巧

原文链接：https://blog.devtang.com/2025/01/05/teaching-notes-of-dp/

发表日期：January 5th 2025, 6:03:48 pm

更新日期：January 20th 2025, 10:49:51 pm

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. 引言
  2. 2. 动态规划解题的核心问题
  3. 3. 教学题目
  4. 4. 例题代码
    1. 4.1. P2842 纸币问题 1
    2. 4.2. P1216 数字三角形
    3. 4.3. P2840 纸币问题 2
    4. 4.4. P2834 纸币问题 3
    5. 4.5. P1048 采药
    6. 4.6. P2196 挖地雷
    7. 4.7. P1434 滑雪
    8. 4.8. P1115 最大子段和
  5. 5. 作业代码
    1. 5.1. P4017 最大食物链计数
    2. 5.2. P2871 Charm Bracelet S
    3. 5.3. P1802 5 倍经验日
    4. 5.4. P1002 过河卒
    5. 5.5. P1064 金明的预算方案
    6. 5.6. P1077 摆花
    7. 5.7. P1164 小A点菜
    8. 5.8. P2392 考前临时抱佛脚
Total : 343
2025
2024
2023
2022
2021
2020
2019
2018
2017
2016
2015
2014
2013
2012
2011
anniversary Git startup writing Interview books Swift blog 投稿 PM cooking supply-chain marketing cspj
iOS shell mac summary iOS weekly