CSPJ 教学思考：数学题

cspj

字数统计: 1.2k阅读时长: 5 min

 2025/04/12 

数学题是信息学竞赛中重要的一类题目，通常包括几何、数论、容斥原理等。

本文将相关的题目归纳整理，用于教学。

几何

P2241 统计方形

本题解法：每个矩形（包括正方形）都可以由一段左边线段和一段上边线段确定。因此，我们只需要枚举所有可能的线段。

对于一个长是 N 宽是 M 的棋盘。

左边的线段长度为 1 的有 N 个，长度为 2 的有 N-1 个，…长度为 N 的有 1 个。
上边的线段长度为 1 的有 M 个，长度为 2 的有 M-1 个，…长度为 M 的有 1 个。

所以:

左边的线段一共有 （1+2+3+...+N）= N*(N+1)/2 个。
上边的线段一共有 （1+2+3+...+M）= M*(M+1)/2 个。
因此，总共有 N*(N+1)/2 * M*(M+1)/2 个矩形。

用相同的办法可以推导正方形的数量，方法如下：

对于左边长度为 1 的线段有 N 个，相应的上边长度为 1 的线段有 M 个。
所以可以构造出 N*M 个边长为 1 的正方形。

同理：

对于左边长度为 2 的线段有 N-1 个，相应的上边长度为 2 的线段有 M-1 个。
所以可以构造出 (N-1)*(M-1) 个边长为 2 的正方形。

以此类推，可以构造出 N*M + (N-1)*(M-1) + (N-2)*(M-2) + (N-M+1)*1 个正方形(N>M)。

另外，需要注意使用 long long 来保存结果。完整的代码如下：

#include <bits/stdc++.h>
using namespace std;
unsigned long long n, m, ans1, ans2;
int main() {
    cin >> n >> m;
    ans1 = n*(n+1)/2 * m*(m+1)/2;
    while (n > 0 && m > 0) {
        ans2 += n*m;
        n--; m--;
    }
    cout  << ans2 << " " << ans1 - ans2 << endl;
    return 0;
}

数论

P1044 栈

这道题可以先用暴力的办法把前面几个数打出来，然后我们能发现数的规律是：1,1,2,5,14,42,132,429,1430,….

这是计算组合中很常见的卡特兰数，卡特兰数有两种公式，第一种公式是：

f(n) = f(n-1) * (4 * n - 2) / (n + 1)

我个人觉得这个公式不太好记。另一个公式是：

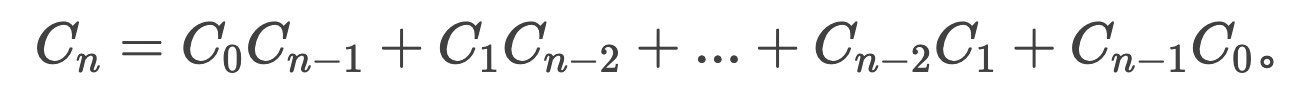
这个递推式相对好记一点：即C(n) = C(0)*C(n-1) + C(1)*C(n-2) ... C(n-1)*C(0)

以下是用该递推式实现的答案：

/**
 * Author: Tang Qiao
 */
#include <bits/stdc++.h>
using namespace std;

long long ans[19];
int main() {
    int n;
    cin >> n;
    ans[0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j < i; ++j) {
            ans[i] += ans[j] * ans[i-1-j];
        }
    }
    cout << ans[n] << endl;
    return 0;
}

P3612 USACO17JAN Secret Cow Code S

这是一道 USACO 的题目，需要我们先找出规律，然后再试图求解。

此题找规律的技巧是分析坐标每次在折半还原时的变化规律。
为了分析规律，我们可以看每次翻倍时，坐标的关系变化。

对于一个长度为 N 的字符串S，每次其长度变为 2*N。所以，我们对每一位进行标号：

1 2 3 4... N N+1 N+2 N+N

其中，除 S[N] == S[N+1] 外（按题意，此项为特殊项），其它位置都符合如下规律：

S[1] == S[N+2]
S[N-1] == S[N+N]

所以，将右边的坐标减去 N 再减 1，就得到左边的坐标。

所以，设总长为 L, 如果 a 的位置在右半侧，则对应到左半侧的坐标关系是：

if (a == L/2+1) a = 1;
else a = a - L/2 - 1;

如此递归下去，直到位置落在最初的长度上。
因为字符下标是从 0 开始，所以下标最后要减 1.

最后注意用 long long 来转换坐标。


#include <bits/stdc++.h>
using namespace std;

string s;
long long a, n;
bool debug = false;

long long di(long long a, long long L) {
    if (debug) {
        // 可用 debug 查看坐标变化过程
        cout << "test a = " << a << ", L = " << L << endl;
    }
    if (a <= n) {
        return a;
    } else {
        // 如果 a 的位置在右半侧，则调整到左半侧
        if (a > L/2) {
            if (a == L/2 + 1) a = L/2;
            else a = a - L/2 - 1;   
        }
        return di(a, L/2);
    }
}

int main() {
    cin >> s >> a;
    n = s.length();

    // 求出开始往回递归时，字符串拼起来的长度 L
    long long L = n;
    while (L < a) L *= 2;

    // 寻找 L 这个长度下，第 a 个字符相当于哪个位置
    int ans = di(a, L);
    cout << s[ans-1] << endl;
    return 0;
}